
【题目】![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上不与点
上不与点![]() 重合的一点,作
重合的一点,作![]() 交边
交边![]() 于
于![]() 点.
点.
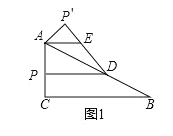
![]() 如图1,将
如图1,将![]() 沿直线
沿直线![]() 翻折,得到
翻折,得到![]() ,作
,作![]() .求证:
.求证:![]() ;
;
![]() 将
将![]() 绕点
绕点![]() 顺时针旋转,得到
顺时针旋转,得到![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]()
①如图2,当点![]() 在
在![]() 内部时,连接
内部时,连接![]() 和
和![]() ,求证:
,求证:![]() ;
;
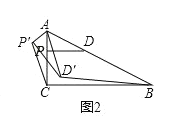
②如果![]() 连接
连接![]() 且
且![]() 那么请直接写出点
那么请直接写出点![]() 到直线
到直线![]() 的距离.
的距离.
【答案】(1)详见解析;(2)①详见解析;②点![]() 到直线
到直线![]() 的距离为
的距离为![]() 或
或![]()
【解析】
(1)由折叠的性质和平行线的性质可得∠EAD=∠ADP=∠ADP',即可得AE=DE;
(2)①由题意可证△APD∽△ACB,可得![]() ,由旋转的性质可得AP=AP',AD=AD',∠PAD=∠P'AD',即∠P'AC=∠D'AB,
,由旋转的性质可得AP=AP',AD=AD',∠PAD=∠P'AD',即∠P'AC=∠D'AB,![]() ,则△AP'C∽△AD'B;
,则△AP'C∽△AD'B;
②分点D'在直线BC的下方和点D'在直线BC的上方两种情况讨论,根据平行线分线段成比例,可求PD=![]() ,通过证明△AMD'≌△DPA,可得AM=PD=
,通过证明△AMD'≌△DPA,可得AM=PD=![]() ,即可求点D'到直线BC的距离.
,即可求点D'到直线BC的距离.
![]() 证明:
证明:![]() 将
将![]() 沿直线
沿直线![]() 翻折,得到
翻折,得到![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]() 旋转,
旋转,
![]() ,
,
![]() ,
,![]()
![]()
![]() 若点
若点![]() 在直线
在直线![]() 下方,如图,过点
下方,如图,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]()

![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]() 旋转,
旋转,
![]() ,且
,且![]()
![]() ,
,![]() ,
,
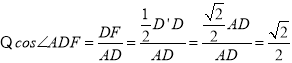
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,且
,且![]()
![]()
![]()
![]() ,
,
![]()
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]()
若点![]() 在直线
在直线![]() 的上方,如图,过点
的上方,如图,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
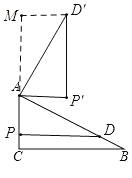
同理可证:![]() ,
,
![]()
![]()
![]()
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]()
综上所述:点![]() 到直线
到直线![]() 的距离为
的距离为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
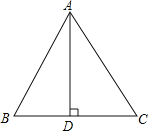
【题目】如图,在等边△ABC中,AB=6,AD是高.
(1)尺规作图:作△ABC的外接圆⊙O(保留作图痕迹,不写作法)
(2)在(1)所作的图中,求线段AD,BD与弧![]() 所围成的封闭图形的面积.
所围成的封闭图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
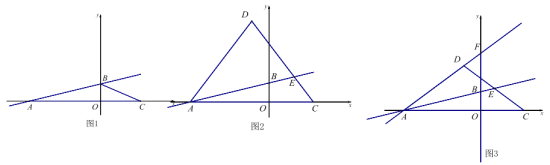
【题目】已知,如图,在平面直角坐标系中,直线AB:![]() 交x轴于点A(-4,0),交y轴于点B,点C(2,0).
交x轴于点A(-4,0),交y轴于点B,点C(2,0).
(1)如图1,求直线AB的解析式;
(2)如图2,点D为第二象限内一点,且AD=DC,DC交直线AB于点E,设DE:EC=m,点D的纵坐标为d,求d与m的函数关系式(不要求写出自变量的取值范围);
(3)如图3,在(2)的条件下,直线AD交y轴于点F,点P为线段AF上一点,G为y轴负半轴上一点,PG=AB,且∠PGF+∠BAF=∠AFB,当m=1时,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家今年3月份两次同时购进了甲、乙两种不同单价的糖果,第一次购买甲种糖果的数量比乙种糖果的数量多50%,第二次购买甲种糖果的数量比第一次购买甲种糖果的数量少60%,结果第二次购买糖果的总数量虽然比第一次购买糖果的总数量多20%,但第二次购买甲乙糖果的总费用却比第一次购买甲乙糖果的总费用费少10%.(甲,乙两种糖果的单价不变),则乙种糖果的单价是甲种糖果单价的_____%.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市促销活动,将A,B,C三种水果采用甲、乙、丙三种方式搭配装进礼盒进行销售.每盒的总成本为盒中A,B,C三种水果成本之和,盒子成本忽略不计.甲种方式每盒分别装A,B,C三种水果6kg,3kg,1kg;乙种方式每盒分别装A,B,C三种水果2kg,6kg,2kg.甲每盒的总成本是每千克A水果成本的12.5倍,每盒甲的销售利润率为20%;每盒甲比每盒乙的售价低25%;每盒丙在成本上提高40%标价后打八折出售,获利为每千克A水果成本的1.2倍.当销售甲、乙、丙三种方式搭配的礼盒数量之比为2:2:5时,则销售总利润率为_____.(利润率=利润÷成本×100%)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )

A. 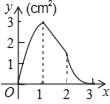 B.
B. 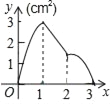 C.
C. 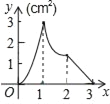 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=8.
(1)作△ABC的内角∠CAB的平分线,与边BC交于点D(用尺规作图,保留作图痕迹,不要求写作法);
(2)若AD=BD,求CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.

小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com