
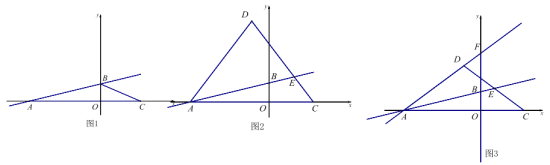
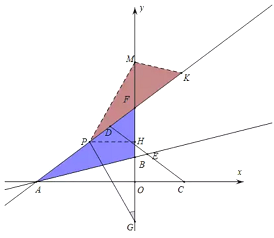
【题目】已知,如图,在平面直角坐标系中,直线AB:![]() 交x轴于点A(-4,0),交y轴于点B,点C(2,0).
交x轴于点A(-4,0),交y轴于点B,点C(2,0).
(1)如图1,求直线AB的解析式;
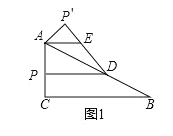
(2)如图2,点D为第二象限内一点,且AD=DC,DC交直线AB于点E,设DE:EC=m,点D的纵坐标为d,求d与m的函数关系式(不要求写出自变量的取值范围);
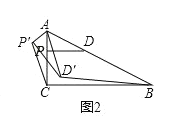
(3)如图3,在(2)的条件下,直线AD交y轴于点F,点P为线段AF上一点,G为y轴负半轴上一点,PG=AB,且∠PGF+∠BAF=∠AFB,当m=1时,求点G的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)将点A(4,0)代入![]() ,求出b=1即可;
,求出b=1即可;
(2)由已知可得D(1,d),求出CD的直线解析式为![]() ,再由E是两直线的交点,求出E(
,再由E是两直线的交点,求出E(![]() ,
,![]() ),过点D作DQ⊥x轴于Q,作EN∥x轴交DQ于N,则
),过点D作DQ⊥x轴于Q,作EN∥x轴交DQ于N,则![]() ,由EC:CD=1:(m+1),即可求出d=
,由EC:CD=1:(m+1),即可求出d=![]() ;
;
(3)过点P作PH⊥y轴于点H,截取HM=HG,求出直线AD的解析式为![]() ,则F(0,3),tan∠AFB=
,则F(0,3),tan∠AFB=![]() ,所以FH=
,所以FH=![]() PH,易证Rt△PHG≌RtPHM,由角的关系得到∠MPF=∠FAB,构造△PKM≌△AFB,可得FB=MK=MF,求出FB=MK=MF=2,在Rt△PHM中,根据PM2=PH2+MH2,求出PH=
PH,易证Rt△PHG≌RtPHM,由角的关系得到∠MPF=∠FAB,构造△PKM≌△AFB,可得FB=MK=MF,求出FB=MK=MF=2,在Rt△PHM中,根据PM2=PH2+MH2,求出PH=![]() ,FH=
,FH=![]() ,最后求出OG=HGOH=
,最后求出OG=HGOH=![]() ,即可求解.
,即可求解.
解:(1)将点A(4,0)代入![]() ,得
,得![]() ,
,
∴b=1,
∴直线AB的解析式为![]() ;
;
(2)∵AC=6,AD=DC,
∴D的横坐标为1,
∵点D的纵坐标为d,
设直线CD的解析式为![]() ,
,
代入D(1,d),C(2,0)得:![]() ,解得:
,解得: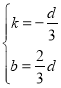 ,
,
∴直线CD的解析式为![]() ,
,
联立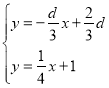 ,可得E(
,可得E(![]() ,
,![]() ),
),

如图,过点D作DQ⊥x轴于Q,作EN∥x轴交DQ于N,
则![]() ,
,
∵DE:EC=m,
∴EC:CD=1:(m+1),
∴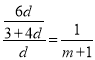 ,
,
∴d=![]() ;
;
(3)如图,过点P作PH⊥y轴于点H,截取HM=HG,
∵m=1,
∴d=![]() ,
,
∴D(1,![]() ),
),
设直线AD的解析式为![]() ,
,
代入A(4,0),D(1,![]() )得:
)得: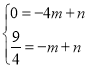 ,解得:
,解得: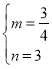 ,
,
∴直线AD的解析式为![]() ,
,
∴F(0,3),
∴tan∠AFB=![]() ,
,
∴![]() ,
,
∴FH=![]() PH,
PH,
易证Rt△PHG≌Rt△PHM(HL),
∴PG=PM=AB,∠PGH=∠PMH,
∴∠AFB=∠PMF+∠MPF,
∵∠PGF+∠BAF=∠AFB,
∴∠MPF=∠FAB,
构造△PKM≌△AFB,
则∠MFK=∠AFB=∠PKM,
∴FB=MK=MF,
∵OF=3,OB=1,
∴FB=MK=MF=2,
在Rt△PHM中,PM2=PH2+MH2,
∵AB=![]() ,
,
∴17=PH2+(2+![]() PH)2,
PH)2,
∴PH=![]() ,
,
∴FH=![]() ,
,
∴HG=HM=2+![]() =
=![]() ,OH=3
,OH=3![]() =
=![]() ,
,
∴OG=HGOH=![]() ,
,
∴G(0,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解旅游人数的变化情况,收集并整理了2017年1月至2019年12月期间的月接待旅游量(单位:万人次)的数据并绘制了统计图如下:
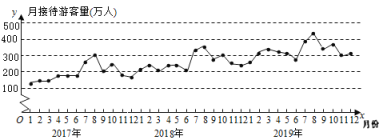
根据统计图提供的信息,下列推断不合理的是( )
A.2017年至2019年,年接待旅游量逐年增加
B.2017年至2019年,各年的月接待旅游量高峰期大致在7,8月份
C.2019年的月接待旅游量的平均值超过300万人次
D.2017年至2019年,各年下半年(7月至12月)的月接待旅游量相对于上半年(1月至6月)波动性更小,变化比较平稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天府新区某校数学活动小组在一次活动中,对一个数学问题作如下探究:
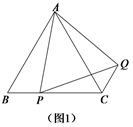
(1)问题发现:如图1,在等边△ABC中,点P是边BC上任意一点,连接AP,以AP为边作等边△APQ,连接CQ.求证:BP CQ;
(2)变式探究:如图2,在等腰△ABC中,ABBC,点P是边BC上任意一点,以AP为腰作等腰△APQ,使AP PQ,APQ ABC,连接CQ.判断∠ABC和∠ACQ的数量关系,并说明理由;
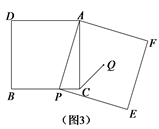
(3)解决问题:如图3,在正方形ADBC中,点P是边BC上一点,以AP为边作正方形 APEF,Q是正方形APEF的中心,连接CQ.若正方形APEF的边长为6,![]() ,求正方形ADBC的边长.
,求正方形ADBC的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上不与点
上不与点![]() 重合的一点,作
重合的一点,作![]() 交边
交边![]() 于
于![]() 点.
点.
![]() 如图1,将
如图1,将![]() 沿直线
沿直线![]() 翻折,得到
翻折,得到![]() ,作
,作![]() .求证:
.求证:![]() ;
;
![]() 将
将![]() 绕点
绕点![]() 顺时针旋转,得到
顺时针旋转,得到![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]()
①如图2,当点![]() 在
在![]() 内部时,连接
内部时,连接![]() 和
和![]() ,求证:
,求证:![]() ;
;
②如果![]() 连接
连接![]() 且
且![]() 那么请直接写出点
那么请直接写出点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
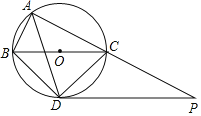
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在 10×6 的正方形网格中,每个小正方形的边长均为 1,线段 AB 的端点 A、B 均在小正方形的顶点上.
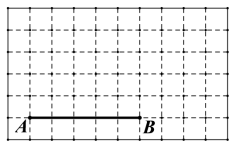
(1)在图中画出以 AB 为一腰的等腰△ABC,点 C 在小正方形顶点上,△ABC 为钝角三角形,且△ABC 的面积为![]() ;
;
(2)在图中画出以 AB 为斜边的直角三角形 ABD, 点 D在小正方形的顶点上,且 AD>BD;
(3)连接 CD,请你直接写出线段 CD 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com