
【题目】如图,在![]() 中,,点
中,,点![]() 在
在![]() 上,且
上,且![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点,连结
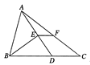
的中点,连结![]() .若四边形DCFE和△BDE的面积都为3,则△ABC的面积为____.
.若四边形DCFE和△BDE的面积都为3,则△ABC的面积为____.
【答案】10
【解析】
首先利用等腰三角形的性质得到点E是AD的中点,可得EF是△ACD的中位线,则EF∥CD,EF=![]() CD,进而可证明△AEF∽△ADC,然后利用相似三角形面积的比等于相似比的平方求得△ADC的面积,由点E是AD的中点得△BDE和△BAE面积相等,利用
CD,进而可证明△AEF∽△ADC,然后利用相似三角形面积的比等于相似比的平方求得△ADC的面积,由点E是AD的中点得△BDE和△BAE面积相等,利用![]()
![]() 即可求解.
即可求解.
解:∵BE平分∠ABC,BD=BA,
∴BE是△ABD的中线,
∴点E是AD的中点,
又∵F是AC的中点,
∴EF是△ADC的中位线,
∴EF∥CD,EF=![]() CD,
CD,
∴△AEF∽△ADC,
∴S△AEF:S△ADC=1:4,
∴S△AEF:S四边形DCFE=1:3,
∵四边形DCFE的面积为3,
∴S△AEF=1,
∴S△ADC =S△AEF+ S四边形DCFE =1+3=4,
∵点E是AD的中点,△BDE的面积为3,
∴ ![]() =3,
=3,
∴![]() =3+3+4=10.
=3+3+4=10.
故答案为:10.


科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+x+b与x轴交于A、B两点,与y轴交于点C.
(1)若B点坐标为(2,0)
①求实数b的值;
②如图1,点E是抛物线在第一象限内的图象上的点,求△CBE面积的最大值及此时点E的坐标.
(2)如图2,抛物线的对称轴交x轴于点D,若抛物线上存在点P,使得P、B、C、D四点能构成平行四边形,求实数b的值.(提示:若点M,N的坐标为M(x,y),N(x,y),则线段MN的中点坐标为(![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G经过点
的图象G经过点![]() ,直线
,直线![]() 与y轴交于点B,与图象G交于点C.
与y轴交于点B,与图象G交于点C.
(1)求m的值.
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点![]() 时,直接写出区域W内的整点个数.
时,直接写出区域W内的整点个数.
②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
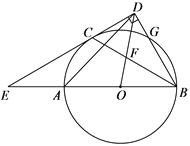
【题目】如图,AB是⊙O的直径,C,G是⊙O上两点,且![]() ,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若![]() ,求证:AE=AO;
,求证:AE=AO;
(3)连接 AD,在(2)的条件下,若CD ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,直线AB:![]() 交x轴于点A(-4,0),交y轴于点B,点C(2,0).
交x轴于点A(-4,0),交y轴于点B,点C(2,0).
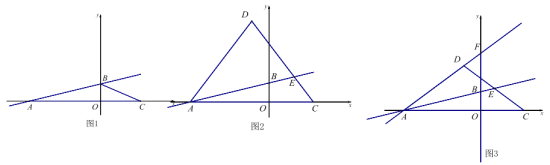
(1)如图1,求直线AB的解析式;
(2)如图2,点D为第二象限内一点,且AD=DC,DC交直线AB于点E,设DE:EC=m,点D的纵坐标为d,求d与m的函数关系式(不要求写出自变量的取值范围);
(3)如图3,在(2)的条件下,直线AD交y轴于点F,点P为线段AF上一点,G为y轴负半轴上一点,PG=AB,且∠PGF+∠BAF=∠AFB,当m=1时,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青山区政府美化城市环境,计划对面积为![]() 平方米的区域进行绿化,安排甲、乙两个工程队完成,已知乙队每天能完成绿化的面积是甲队每天能完成绿化面积的
平方米的区域进行绿化,安排甲、乙两个工程队完成,已知乙队每天能完成绿化的面积是甲队每天能完成绿化面积的![]() 倍,并且在独立完成面积为平
倍,并且在独立完成面积为平![]() 方米区域的绿化时,甲队比乙队多用
方米区域的绿化时,甲队比乙队多用![]() 天.
天.
![]() 求甲、乙两工程队每天能完成绿化的面积分别是多少平方米?
求甲、乙两工程队每天能完成绿化的面积分别是多少平方米?
![]() 若区政府每天需付给甲队的绿化费用为
若区政府每天需付给甲队的绿化费用为![]() 万元,乙队为
万元,乙队为![]() 万元,要使这次的绿化总费用不超过
万元,要使这次的绿化总费用不超过![]() 万元,至少应安排甲队工作多少天?
万元,至少应安排甲队工作多少天?
![]() 为合理利用绿化用地,这是需要用长为
为合理利用绿化用地,这是需要用长为![]() 米的植物隔离带靠着墙(墙的最大可用长度为
米的植物隔离带靠着墙(墙的最大可用长度为![]() 是
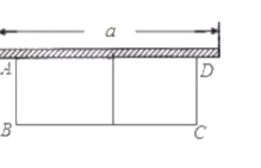
是![]() 米,植物隔离带的自身宽度不计),如图所示,围成中间隔有植物隔离带的长方形中央绿地,设绿地的宽
米,植物隔离带的自身宽度不计),如图所示,围成中间隔有植物隔离带的长方形中央绿地,设绿地的宽![]() 为
为![]() 米,面积为
米,面积为![]() 米
米![]() .试问中央绿地的面积能达到
.试问中央绿地的面积能达到![]() 吗?如果能,请求出此时
吗?如果能,请求出此时![]() 的长;如果不能,请说明理由.
的长;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市促销活动,将A,B,C三种水果采用甲、乙、丙三种方式搭配装进礼盒进行销售.每盒的总成本为盒中A,B,C三种水果成本之和,盒子成本忽略不计.甲种方式每盒分别装A,B,C三种水果6kg,3kg,1kg;乙种方式每盒分别装A,B,C三种水果2kg,6kg,2kg.甲每盒的总成本是每千克A水果成本的12.5倍,每盒甲的销售利润率为20%;每盒甲比每盒乙的售价低25%;每盒丙在成本上提高40%标价后打八折出售,获利为每千克A水果成本的1.2倍.当销售甲、乙、丙三种方式搭配的礼盒数量之比为2:2:5时,则销售总利润率为_____.(利润率=利润÷成本×100%)
查看答案和解析>>
科目:初中数学 来源: 题型:
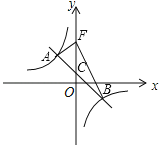
【题目】在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=![]() (k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
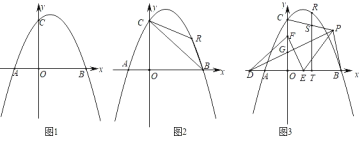
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com