
【题目】青山区政府美化城市环境,计划对面积为![]() 平方米的区域进行绿化,安排甲、乙两个工程队完成,已知乙队每天能完成绿化的面积是甲队每天能完成绿化面积的
平方米的区域进行绿化,安排甲、乙两个工程队完成,已知乙队每天能完成绿化的面积是甲队每天能完成绿化面积的![]() 倍,并且在独立完成面积为平
倍,并且在独立完成面积为平![]() 方米区域的绿化时,甲队比乙队多用
方米区域的绿化时,甲队比乙队多用![]() 天.
天.
![]() 求甲、乙两工程队每天能完成绿化的面积分别是多少平方米?
求甲、乙两工程队每天能完成绿化的面积分别是多少平方米?
![]() 若区政府每天需付给甲队的绿化费用为
若区政府每天需付给甲队的绿化费用为![]() 万元,乙队为
万元,乙队为![]() 万元,要使这次的绿化总费用不超过
万元,要使这次的绿化总费用不超过![]() 万元,至少应安排甲队工作多少天?
万元,至少应安排甲队工作多少天?
![]() 为合理利用绿化用地,这是需要用长为
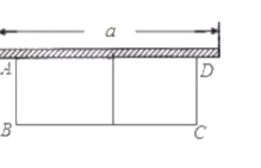
为合理利用绿化用地,这是需要用长为![]() 米的植物隔离带靠着墙(墙的最大可用长度为
米的植物隔离带靠着墙(墙的最大可用长度为![]() 是
是![]() 米,植物隔离带的自身宽度不计),如图所示,围成中间隔有植物隔离带的长方形中央绿地,设绿地的宽
米,植物隔离带的自身宽度不计),如图所示,围成中间隔有植物隔离带的长方形中央绿地,设绿地的宽![]() 为
为![]() 米,面积为
米,面积为![]() 米
米![]() .试问中央绿地的面积能达到
.试问中央绿地的面积能达到![]() 吗?如果能,请求出此时
吗?如果能,请求出此时![]() 的长;如果不能,请说明理由.
的长;如果不能,请说明理由.
【答案】(1)甲工程队每天能完成绿化的面积是![]() 平方米,乙工程队每天能完成绿化的面积是
平方米,乙工程队每天能完成绿化的面积是![]() 平方米;(2)至少应安排甲队工作
平方米;(2)至少应安排甲队工作![]() 天;(3)花圃的面积不能达到
天;(3)花圃的面积不能达到![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)设甲工程队每天能完成绿化的面积是x平方米,则乙工程队每天能完成绿化的面积是1.5x平方米,根据工作时间=工作总量÷工作效率结合在独立完成面积为450平方米区域的绿化时甲队比乙队多用5天,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设安排甲队工作m天,则需安排乙队工作![]() 天,根据总费用=0.3×甲队工作时间+0.9×乙队工作时间结合这次的绿化总费用不超过24万元,即可得出关于m的一元一次不等式,解之取其最小值即可得出结论;
天,根据总费用=0.3×甲队工作时间+0.9×乙队工作时间结合这次的绿化总费用不超过24万元,即可得出关于m的一元一次不等式,解之取其最小值即可得出结论;
(3)求出中央绿地的面积为![]() ,根据二次函数的性质即可判断.
,根据二次函数的性质即可判断.
解:![]() 设甲工程队每天能完成绿化的面积是
设甲工程队每天能完成绿化的面积是![]() 平方米,
平方米,
则乙工程队每天能完成绿化的面积是![]() 平方米,
平方米,
依题意,得: ![]() ,
,
解得:![]() ,
,
经检验,![]() 是原方程的解,且符合题意,
是原方程的解,且符合题意,
![]() .
.
答:甲工程队每天能完成绿化的面积是![]() 平方米,乙工程队每天能完成绿化的面积是
平方米,乙工程队每天能完成绿化的面积是![]() 平方米.
平方米.
![]() 设安排甲队工作
设安排甲队工作![]() 天,则需安排乙队工作
天,则需安排乙队工作![]() 天,
天,
依题意,得:![]()
解得:![]() .
.
答:至少应安排甲队工作![]() 天.
天.
![]() 中央绿地的面积为
中央绿地的面积为![]()
![]() 当
当![]() 长为
长为![]() ,宽为
,宽为![]() 时,有最大面积,为
时,有最大面积,为![]() 平方米
平方米
又![]() 当
当![]() 时,长方形中央绿地的长为
时,长方形中央绿地的长为![]() 米,
米,
又墙的最大可用长度![]() 是
是![]() ,故舍去;
,故舍去;
故花圃的面积不能达到![]() .
.


科目:初中数学 来源: 题型:
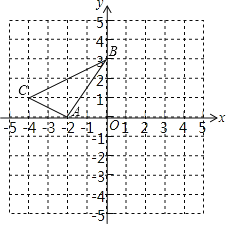
【题目】如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,3),C(﹣4,1).以原点O为旋转中心,将△ABC顺时针旋转90°得到△A'B'C',其中点A,B,C旋转后的对应点分别为点A',B',C'.
(1)画出△A'B'C',并写出点A',B',C'的坐标;
(2)求经过点B',B,A三点的抛物线对应的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于给定的![]() ,我们给出如下定义:若点M是边
,我们给出如下定义:若点M是边![]() 上的一个定点,且以M为圆心的半圆上的所有点都在
上的一个定点,且以M为圆心的半圆上的所有点都在![]() 的内部或边上,则称这样的半圆为
的内部或边上,则称这样的半圆为![]() 边上的点M关于
边上的点M关于![]() 的内半圆,并将半径最大的内半圆称为点M关于
的内半圆,并将半径最大的内半圆称为点M关于![]() 的最大内半圆.若点M是边
的最大内半圆.若点M是边![]() 上的一个动点(M不与B,C重合),则在所有的点M关于
上的一个动点(M不与B,C重合),则在所有的点M关于![]() 的最大内半圆中,将半径最大的内半圆称为
的最大内半圆中,将半径最大的内半圆称为![]() 关于
关于![]() 的内半圆.
的内半圆.
(1)在![]() 中,
中,![]() ,
,![]() ,
,
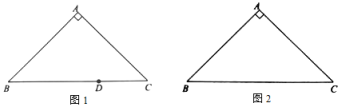
①如图1,点D在边![]() 上,且
上,且![]() ,直接写出点D关于
,直接写出点D关于![]() 的最大内半圆的半径长;
的最大内半圆的半径长;
②如图2,画出![]() 关于
关于![]() 的内半圆,并直接写出它的半径长;
的内半圆,并直接写出它的半径长;
(2)在平面直角坐标系![]() 中,点E的坐标为
中,点E的坐标为![]() ,点P在直线
,点P在直线![]() 上运动(P不与O重合),将
上运动(P不与O重合),将![]() 关于
关于![]() 的内半圆半径记为R,当
的内半圆半径记为R,当![]() 时,求点P的横坐标t的取值范围.
时,求点P的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品经销店欲购进A、B两种纪念品,用320元购进的A种纪念品与用400元购进的B种纪念品的数量相同,每件B种纪念品的进价比A种纪念品的进价贵10元.
(1)求A、B两种纪念品每件的进价分别为多少?
(2)若该商店A种纪念品每件售价45元,B种纪念品每件售价60元,这两种纪念品共购进200件,这两种纪念品全部售出后总获利不低于1600元,求A种纪念品最多购进多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P在函数y=![]() (x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣
(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣![]() (x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
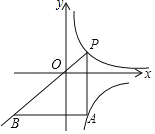
A.逐渐变大B.逐渐变小C.等于定值16D.等于定值24
查看答案和解析>>
科目:初中数学 来源: 题型:
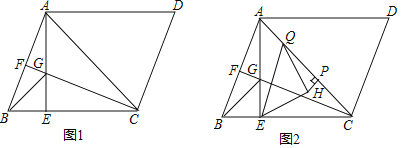
【题目】已知平行四边形![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,且满足
,且满足![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
(2)如图2取![]() 上一点
上一点![]() ,连接
,连接![]() ,在
,在![]() 内取一点
内取一点![]() ,连接
,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,若
,若![]() ,
,![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
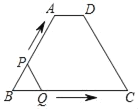
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=2,BC=8,点P从点B出发沿折线BA﹣AD﹣DC匀速运动,同时,点Q从点B出发沿折线BC﹣CD匀速运动,点P与点Q的速度相同,当二者相遇时,运动停止,设点P运动的路程为x,△BPQ的面积为y,则y关于x的函数图象大致是( )
A.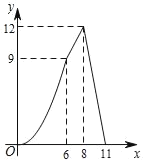 B.
B.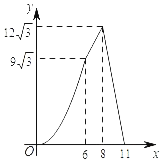
C.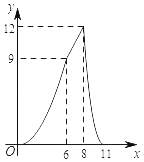 D.
D.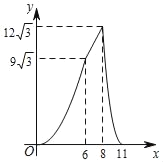
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二十四届冬季奧林匹克运动会将于2022年2月4日至2月20日在北京举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有![]() 名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
[收集数据]
从甲、乙两校各随机抽取![]() 名学生,在这次竞赛中他们的成绩如下:
名学生,在这次竞赛中他们的成绩如下:
甲:![]()
![]()
乙:![]()
![]()
[整理、描述数据]按如下分数段整理、描述这两组样本数据:
学校 人数 成绩 |
|
|
|
甲 |
|
|
|
乙 |
|
|
|
(说明:优秀成绩为![]() ,良好成绩为
,良好成绩为![]() 合格成绩为
合格成绩为![]() .)
.)
[分析数据]两组样本数据的平均分、中位数、众数如下表所示:
学校 | 平均分 | 中位数 | 众数 |
甲 |
|
|
|
乙 |
|
|
|
其中![]() .
.
[得出结论]
(1)小明同学说:“这次竞赛我得了![]() 分,在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生;(填“甲”或“乙”)
分,在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生;(填“甲”或“乙”)
(2)张老师从乙校随机抽取--名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为_ ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由: ;
(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com