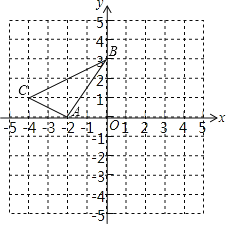
【题目】如图，在平面直角坐标系xOy中，A（﹣2，0），B（0，3），C（﹣4，1）．以原点O为旋转中心，将△ABC顺时针旋转90°得到△A'B'C'，其中点A，B，C旋转后的对应点分别为点A'，B'，C'．
（1）画出△A'B'C'，并写出点A'，B'，C'的坐标；
（2）求经过点B'，B，A三点的抛物线对应的函数解析式．
科目：初中数学 来源： 题型：
【题目】小明经过市场调查，整理出他妈妈商店里一种商品在第
天的销售量的相关信息如下表：
时间第 |
|
|
售价（元/件） |
| 50 |
每天销量（件） |
| |
已知该商品的进价为每件20元，设销售该商品的每天利润为
元.
（1）求出与
的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于2400元？请直接写出结果.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的边长是3，BP=CQ，连接AQ，DP交于点O，并分别与边CD，BC交于点F，E，连接AE，下列结论：①AQ⊥DP；②OA2=OEOP；③S△AOD=S四边形OECF；④当BP=1时，tan∠OAE=
，其中正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A（﹣1，﹣1），点B（1，1），若抛物线y＝x2﹣ax+a+1与线段AB有两个不同的交点（包含线段AB端点），则实数a的取值范围是（ ）
A.
≤a＜﹣1B.≤a≤﹣1C.＜a＜﹣1D.＜a≤﹣1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y＝﹣x2+x+b与x轴交于A、B两点，与y轴交于点C．
（1）若B点坐标为（2，0）
①求实数b的值；
②如图1，点E是抛物线在第一象限内的图象上的点，求△CBE面积的最大值及此时点E的坐标．
（2）如图2，抛物线的对称轴交x轴于点D，若抛物线上存在点P，使得P、B、C、D四点能构成平行四边形，求实数b的值．（提示：若点M，N的坐标为M（x，y），N（x，y），则线段MN的中点坐标为（
，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】疫情防控，我们一直在坚守．某居委会组织两个检查组，分别对“居民体温”和“居民安全出行”的情况进行抽查．若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查，则他们恰好抽到同一个小区的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：连结菱形的一边中点与对边的两端点的线段把它分成三个三角形，如果其中有两个三角形相似，那么称这样的菱形为自相似菱形．
(1)判断下列命题是真命题，还是假命题？
①正方形是自相似菱形；
②有一个内角为60°的菱形是自相似菱形．
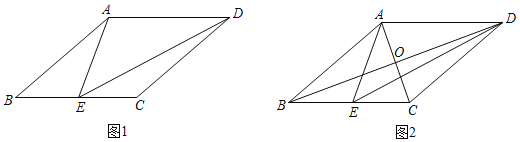
③如图1，若菱形ABCD是自相似菱形，∠ABC=α(0°＜α＜90°)，E为BC中点，则在△ABE，△AED，△EDC中，相似的三角形只有△ABE与△AED．
(2)如图2，菱形ABCD是自相似菱形，∠ABC是锐角，边长为4，E为BC中点．
①求AE，DE的长；
②AC，BD交于点O，求tan∠DBC的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】青山区政府美化城市环境，计划对面积为
平方米的区域进行绿化，安排甲、乙两个工程队完成，已知乙队每天能完成绿化的面积是甲队每天能完成绿化面积的
倍，并且在独立完成面积为平
方米区域的绿化时，甲队比乙队多用
天．
求甲、乙两工程队每天能完成绿化的面积分别是多少平方米？
若区政府每天需付给甲队的绿化费用为
万元，乙队为
万元，要使这次的绿化总费用不超过
万元，至少应安排甲队工作多少天？
为合理利用绿化用地，这是需要用长为米的植物隔离带靠着墙(墙的最大可用长度为
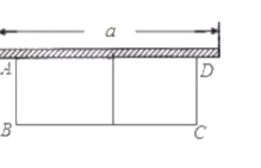
是
米，植物隔离带的自身宽度不计)，如图所示，围成中间隔有植物隔离带的长方形中央绿地，设绿地的宽
为
米，面积为
米
．试问中央绿地的面积能达到
吗？如果能，请求出此时的长；如果不能，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
