
����Ŀ��С�������г����飬�������������̵���һ����Ʒ�ڵ�![]() ����������������Ϣ���±���
����������������Ϣ���±���
ʱ��� |
|
|
�ۼۣ�Ԫ/���� |
| 50 |
ÿ������������ |
| |
��֪����Ʒ�Ľ���Ϊÿ��20Ԫ�������۸���Ʒ��ÿ������Ϊ![]() Ԫ.
Ԫ.
��1�����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������2400Ԫ����ֱ��д�����.
���𰸡���1��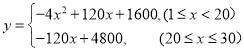 ����2��15��ʱ�������������������������Ϊ2500Ԫ����3��11
����2��15��ʱ�������������������������Ϊ2500Ԫ����3��11
��������
��1����������=ÿ�������������۵ļ�����������ú����Ľ���ʽ��
��2�����ݣ�1���õ�����������ʽ����϶��κ�����һ�κ��������ʿɷֱ�ó����ֵ�������������ıȽϣ��ɵô𰸣�
��3�����ݶ��κ���ֵ���ڻ����2400��һ�κ���ֵ���ڻ����2400���ɵò���ʽ�����ݽⲻ��ʽ���ɵô𰸣�
�⣺(1)��![]() ʱ��
ʱ��
![]() ��
��
��![]() ʱ��
ʱ��
![]() ��
��
���ϣ�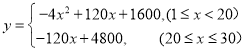
��2����![]() ʱ��
ʱ��
![]()
��![]() ��
��
�൱![]() ʱ��
ʱ��![]() �����ֵ�����ֵΪ2500Ԫ
�����ֵ�����ֵΪ2500Ԫ
��![]() ʱ��
ʱ��
![]() .
.
��![]() ��
��
��![]() ��
��![]() ���������С.
���������С.
�൱![]() ʱ��
ʱ��![]() �����ֵ�����ֵΪ2400Ԫ��
�����ֵ�����ֵΪ2400Ԫ��
���Ͽ�֪����![]() ʱ�������������������������Ϊ2500Ԫ.
ʱ�������������������������Ϊ2500Ԫ.
��3���ٵ�1��x��20ʱ��y=-4x2+120x+1600��2400��
��ã�10��x��20��
���������2400Ԫ��������10��x��20����10�죻
�ڵ�20��x��30ʱ��y=-120x+4800��2400��
��ã�x��20��
���������2400Ԫ��������20��x��20����1�죬
���Ը���Ʒ���������۹����У���11��ÿ������������2400Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
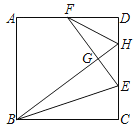
����Ŀ����ͼ��������ֽƬABCD��ֱ��BE�۵�����Cǡ�����ڵ�G��������BG���ӳ�����CD�ڵ�H���ӳ�EG��AD�ڵ�F������FH����AF��FD��6cm����FH�ij�Ϊ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
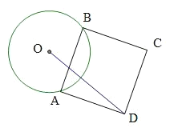
����Ŀ����ͼ����O �İ뾶Ϊ 3��AB ΪԲ��һ���ң��� AB Ϊ���������� ABCD���� OD �����ֵ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ���ı���ABCD�У���O����ABC�����Բ��CD���O�����ڵ�C����P���ӻ�BC�ϵ�һ�����㣨��P�����B��C�غϣ�������PA��PB��PC��
��1����֤��![]() ��
��
��2����![]() ʱ�����ж���APC����CBA�Ƿ�ȫ�ȣ���˵�����ɣ�
ʱ�����ж���APC����CBA�Ƿ�ȫ�ȣ���˵�����ɣ�
��3����գ���![]() �Ķ���Ϊ_________ʱ���ı���ABCD�����Σ�
�Ķ���Ϊ_________ʱ���ı���ABCD�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ������1�³���20000Ԫ/Ķ�ļ۸�а���10Ķ��������ֲijũ�����֪������ͳ��ֲ��ÿ��ÿĶ�ܲ���3000ǧ�ˣ�ÿĶ����ֲ����Ϊ2500Ԫ��������ѧ��ֲ��ÿ��ÿĶ����������![]() ������ֲ���û�����2000Ԫ/Ķ����ǰ����Ҫ��Ͷ��25��Ԫ������4���µ�ʱ��������������ĸ��ƣ������ڼ�����ֲ����֪ÿǧ��ũ�����г��ۼ�Ϊ3Ԫ��ÿ�µ�һ����ȫ�����ۣ�����ǰ
������ֲ���û�����2000Ԫ/Ķ����ǰ����Ҫ��Ͷ��25��Ԫ������4���µ�ʱ��������������ĸ��ƣ������ڼ�����ֲ����֪ÿǧ��ũ�����г��ۼ�Ϊ3Ԫ��ÿ�µ�һ����ȫ�����ۣ�����ǰ![]() ���������ܶ�Ϊ
���������ܶ�Ϊ![]() ����Ԫ����
����Ԫ����
��1����![]() ʱ���ֱ����������ֲ�����µ������ܶ�
ʱ���ֱ����������ֲ�����µ������ܶ�![]() ��
��
��2���ʣ�����ũ��ѡ���ѧ��ֲ�������º��ܹ��ջسɱ���
��3���ڣ�2���������£������2019��1�³�������ô����Ҫ����ʱ����ũ����õ��������ܹ�������ͳ��ֲͬ��ʱ��������õ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���ٰ조�Ļ��ж���Т����ĸ���Ļ��Ϊ�ˣ�Уѧ�����ȫУ1 000��ͬѧ����ڼ�ƽ��ÿ����������ʱ�䣬�����ȡ����ͬѧ���е��飬�����Ƴ���������ͳ��ͼ��
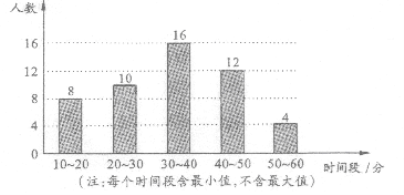
��1�����ε����ȡ������Ϊ_______������ȫУͬѧ������ڼ�ƽ��ÿ����������ʱ����40��������(��40����)������Ϊ_______��
��2��Уѧ�������ڱ���ͻ���ļס��ҡ�����������ͬѧ�У������ȡ����ͬѧ��ȫУ�㱨��������״ͼ���б�����ʾ�����п��ܵĽ��������ǡ�ó鵽�ס�������ͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ����͵�Ϊ D(0��2)
����͵�Ϊ D(0��2)
��1���� m�� n ��ֵ
��2��ֱ�� y��kx��4 �� y ���ڵ� F���������߽��� A��B ���㣬ֱ�� AD �� x ���ڵ� P��
����֤��BP//y ��
���� BQ��AD �� y ���ڵ� Q����֤������ÿ��������ʵ�� k���ı��� FQPB ��Ϊƽ���ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�BC��2��CD��1����ADΪֱ���İ�ԲO��BC�����ڵ�E������BD������Ӱ���ֵ����Ϊ��������
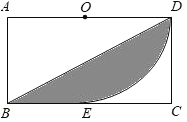
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
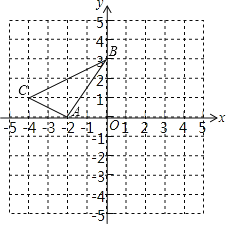
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A����2��0����B��0��3����C����4��1������ԭ��OΪ��ת���ģ�����ABC˳ʱ����ת90��õ���A'B'C'�����е�A��B��C��ת��Ķ�Ӧ��ֱ�Ϊ��A'��B'��C'��
��1��������A'B'C'����д����A'��B'��C'�����ꣻ
��2������B'��B��A����������߶�Ӧ�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com