
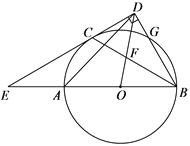
【题目】如图,AB是⊙O的直径,C,G是⊙O上两点,且![]() ,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若![]() ,求证:AE=AO;
,求证:AE=AO;
(3)连接 AD,在(2)的条件下,若CD ![]() ,求AD的长.
,求AD的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)要证明CD是⊙O的切线,连接OC,只要证明∠OCE=90°即可,根据题目中的条件,可以证明OC∥BD,根据CD⊥BG于点D,从而可以证明结论成立;
(2)根据OC∥BD可得![]() ,
,![]() ,利用相似三角形的性质求出
,利用相似三角形的性质求出![]() ,即可证明AE=AO;
,即可证明AE=AO;
(3)在(2)的条件下,根据含30度直角三角形的性质求出半径![]() ,然后作
,然后作![]() 于点
于点![]() ,分别求出DM和AM,根据勾股定理可以求得AD的长.
,分别求出DM和AM,根据勾股定理可以求得AD的长.
解:(1)连接![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的半径,
的半径,
![]() 是
是![]() 的切线;
的切线;
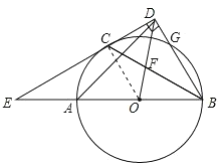
(2)由(1)知,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)在(2)的条件下,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
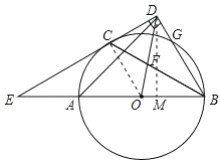
作![]() 于点
于点![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】下表是二次函数![]() 的
的![]() 的部分对应值:
的部分对应值:
| ··· |
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
| ··· |
则对于该函数的性质的判断:
①该二次函数有最小值;
②不等式![]() 的解集是
的解集是![]() 或
或![]()
③方程![]() 的实数根分别位于
的实数根分别位于![]() 和
和![]() 之间;
之间;
④当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;
的增大而增大;
其中正确的是:
A.①②③B.②③C.①②D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备购进一批产品进行销售,该产品的进货单价为6元/个.根据市场调查,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.关于日销售量y(个)与销售单价x(元/个)的几组数据如表:
x | 10 | 12 | 14 | 16 |
y | 300 | 240 | 180 | m |
(1)求出y与x之间的函数关系式(不要求写出自变量的取值范围)及m的值.
(2)按照(1)中的销售规律,当销售单价定为17.5元/个时,日销售量为 个,此时,获得日销售利润是 .
(3)为防范风险,该公司将日进货成本控制在900(含900元)以内,按照(1)中的销售规律,要使日销售利润最大,则销售单价应定为多少?并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是⊙O 外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
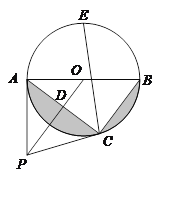
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是![]() 的中点,连接CE,求CE的长.
的中点,连接CE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天府新区某校数学活动小组在一次活动中,对一个数学问题作如下探究:
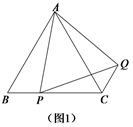
(1)问题发现:如图1,在等边△ABC中,点P是边BC上任意一点,连接AP,以AP为边作等边△APQ,连接CQ.求证:BP CQ;
(2)变式探究:如图2,在等腰△ABC中,ABBC,点P是边BC上任意一点,以AP为腰作等腰△APQ,使AP PQ,APQ ABC,连接CQ.判断∠ABC和∠ACQ的数量关系,并说明理由;
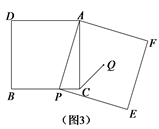
(3)解决问题:如图3,在正方形ADBC中,点P是边BC上一点,以AP为边作正方形 APEF,Q是正方形APEF的中心,连接CQ.若正方形APEF的边长为6,![]() ,求正方形ADBC的边长.
,求正方形ADBC的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现问题:
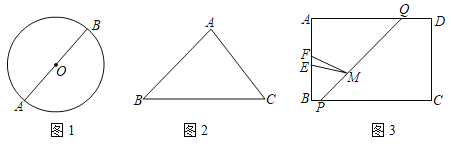
(1)如图1,AB为⊙O的直径,请在⊙O上求作一点P,使∠ABP=45°.(不必写作法)
问题探究:
(2)如图2,等腰直角三角形△ABC中,∠A=90°,AB=AC=3![]() ,D是AB上一点,AD=2
,D是AB上一点,AD=2![]() ,在BC边上是否存在点P,使∠APD=45°?若存在,求出BP的长度,若不存在,请说明理由.
,在BC边上是否存在点P,使∠APD=45°?若存在,求出BP的长度,若不存在,请说明理由.
问题解决:
(3)如图3,为矩形足球场的示意图,其中宽AB=66米、球门EF=8米,且EB=FA.点P、Q分别为BC、AD上的点,BP=7米,∠BPQ=135,一位左前锋球员从点P处带球,沿PQ方向跑动,球员在PQ上的何处才能使射门角度(∠EMF)最大?求出此时PM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4cm,动点E从点A出发,以1cm/秒的速度沿折线AB—BC的路径运动,到点C停止运动.过点E作 EF∥BD,EF与边AD(或边CD)交于点F,EF的长度y(cm)与点E的运动时间x(秒)的函数图象大致是

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com