
【题目】发现问题:
(1)如图1,AB为⊙O的直径,请在⊙O上求作一点P,使∠ABP=45°.(不必写作法)
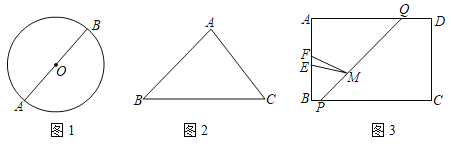
问题探究:
(2)如图2,等腰直角三角形△ABC中,∠A=90°,AB=AC=3![]() ,D是AB上一点,AD=2
,D是AB上一点,AD=2![]() ,在BC边上是否存在点P,使∠APD=45°?若存在,求出BP的长度,若不存在,请说明理由.
,在BC边上是否存在点P,使∠APD=45°?若存在,求出BP的长度,若不存在,请说明理由.
问题解决:
(3)如图3,为矩形足球场的示意图,其中宽AB=66米、球门EF=8米,且EB=FA.点P、Q分别为BC、AD上的点,BP=7米,∠BPQ=135,一位左前锋球员从点P处带球,沿PQ方向跑动,球员在PQ上的何处才能使射门角度(∠EMF)最大?求出此时PM的长度.
【答案】(1)如图所示,见解析;(2)存在.BP=3+![]() 或BP=3﹣
或BP=3﹣![]() ;(3)当球员在PQ上距离点P(12
;(3)当球员在PQ上距离点P(12![]() ﹣7
﹣7![]() )米时,才能使射门角度最大,PM的长度为(12
)米时,才能使射门角度最大,PM的长度为(12![]() ﹣7
﹣7![]() )米.
)米.
【解析】
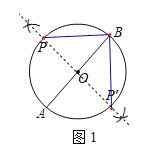
(1)如图1所示.作直径AB的垂直平分线,交⊙O于点P和点P',则点P和点P'即为所求;
(2)如图2和图2'所示:证明△BPD∽△CAP,根据相似三角形的性质得出比例式,设BP=x,则PC=6-x,解方程,方程的解即为BP的长度;
(3)先证明一个基本事实:一条弧所对的圆周角大于圆外角;再在图3中过点E、F作⊙O,使⊙O与PQ相切于点M,则此时∠EMF最大;延长AB、QP交于点N,证明△NEM∽△NMF,利用相似三角形的性质得出比例式,计算即可解得PM的长.
(1)如图所示:作AB的垂直平分线交⊙O于点P、P',则点P或P'即为所求;
(2)存在.
如图2和图2'所示:
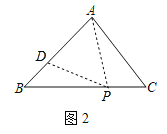
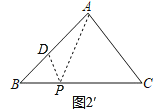
在△ABC中
∵∠BAC=90°,AB=AC=3![]() ,AD=2
,AD=2![]() ,
,
∴∠B=∠C=45°,BD=![]() ,BC=
,BC=![]() AB=6,
AB=6,
∴∠BDP+∠BPD=135°.
∵∠APD=45°,
∴∠APC+∠BPD=135°,
∴∠BDP=∠APC,
∴△BPD∽△CAP
∴![]() =
=![]() .
.
设BP=x,则PC=6﹣x,
∴![]() =
=![]() ,
,
解得x1=3+![]() ,x2=3﹣
,x2=3﹣![]() ,
,
∴BP=3+![]() 或BP=3﹣
或BP=3﹣![]() ;
;
(3)先证明以下事实:若点A、E、F、G均在⊙O'上,点G'为⊙O'外一点,则∠G>∠G'
证明:如图所示,连接AF,
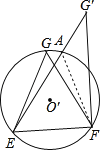
∵∠G=∠EAF,∠EAF>∠G',
∴∠G>∠G',即一条弧所对的圆周角大于圆外角.
如图3,过点E、F作⊙O,使⊙O与PQ相切于点M,由圆周角大于圆外角可知此时∠EMF最大.
(3)如图3,为矩形足球场的示意图,其中宽AB=66米、球门EF=8米,且EB=FA.点P、Q分别为BC、AD上的点,BP=7米,∠BPQ=135,一位左前锋球员从点P处带球,沿PQ方向跑动,球员在PQ上的何处才能使射门角度(∠EMF)最大?求出此时PM的长度.
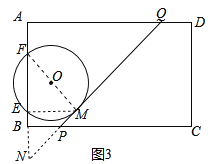
∵AB=66米、EF=8米,EB=FA,
∴EB=29米,
延长AB、QP交于点N,
∵∠BPQ=135°,
∴∠BPN=45°,
∵BN=BP=7,PN=![]() BP=7
BP=7![]() ,NE=36,NF=44米,
,NE=36,NF=44米,
∵∠N=∠N,∠NEM=∠NMF=90°,
∴△NEM∽△NMF,
∴![]() =
=![]() ,
,
∴NM2=NENF,
∴NM=12![]() 米,
米,
∴PM=NM﹣PN=(12![]() ﹣7
﹣7![]() )米.
)米.
答:当球员在PQ上距离点P为(12![]() ﹣7
﹣7![]() )米时,才能使射门角度最大,即PM的长度为(12/span>
)米时,才能使射门角度最大,即PM的长度为(12/span>![]() ﹣7
﹣7![]() )米.
)米.


科目:初中数学 来源: 题型:
【题目】如图1,在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,在菱形
,在菱形![]() 的外部以
的外部以![]() 为边作等边三角形
为边作等边三角形![]() .点
.点![]() 是对角线
是对角线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
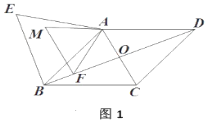
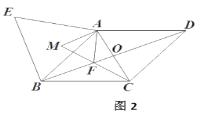
(1)线段![]() 的长为__________;
的长为__________;
(2)如图2,当点![]() 在线段
在线段![]() 上,且点
上,且点![]() ,
,![]() ,
,![]() 三点在同一条直线上时,求证:
三点在同一条直线上时,求证: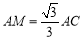 ;
;
(3)连接![]() .若
.若![]() 的周长为
的周长为![]() ,请直接写出
,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=![]() ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
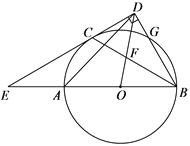
【题目】如图,AB是⊙O的直径,C,G是⊙O上两点,且![]() ,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若![]() ,求证:AE=AO;
,求证:AE=AO;
(3)连接 AD,在(2)的条件下,若CD ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校草根文学社为了了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集,从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:分)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理下分段整理样本数据并补全表格.
课外阅读时间x(分) | 0≤x<40 | 40≤x<80 | 80≤x<120 | 120≤x<160 |
等级 | D | C | B | A |
人数 | 3 |
| 8 |
|
分析数据:补全下列表格中的统计量.
平均数 | 中位数 | 众数 |
80 |
|
|
得出结论:
(1)用样本中的统计量估计我校学生每周用于课外阅读时间的情况等级为 ;
(2)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的平均数估计我校学生每人一年(按52周计算)平均阅读多少本课外书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大润发”、“世纪联华”两家超市出售同样的洗衣液和香皂,洗衣液和香皂在两家超市的售价分别一样.已知买1袋洗衣液和2块香皂要花费48元,买3袋洗衣液和4块香皂要花费134元.
(1)一袋洗衣液与一块香皂售价各是多少元?(列方程组求解)
(2)为了迎接“五一劳动节”,两家超市都在搞促销活动,“大润发”超市规定:这两种商品都打八五折;“世纪联华”超市规定:买一袋洗衣液赠送一块香皂.若妈妈想要买4袋洗衣液和10块香皂,又只能在一家超市购买,你觉得选择哪家超市购买更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
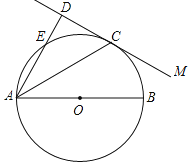
【题目】如图,AB是⊙O的直径,直线MC与⊙O相切于点C.过点A作MC的垂线,垂足为D,线段AD与⊙O相交于点E.
(1)求证:AC是∠DAB的平分线;
(2)若AB=10,AC=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
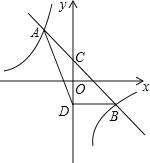
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C,BD垂直于y轴于点D.
的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C,BD垂直于y轴于点D.
(1)求一次函数与反比例函数的表达式;
(2)求△ABD的面积;
(3)若M(x,y)、N(x,y)是反比例函数y=![]() 上的两点,当x<x<0时,直接写出y与y的大小关系
上的两点,当x<x<0时,直接写出y与y的大小关系
查看答案和解析>>
科目:初中数学 来源: 题型:
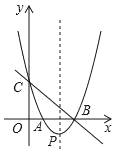
【题目】如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式;
(2)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值;
(3)在该抛物线的对称轴上是否存在点M,使以C、P、M为顶点的三角形为等腰三角形?若存在,请写出所符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com