
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
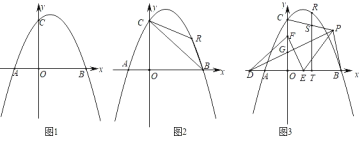
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
【答案】(1)y=﹣![]() x2+x+4;(2)s=﹣t2+4t;(3)当a=1时,R(2,4),当a=
x2+x+4;(2)s=﹣t2+4t;(3)当a=1时,R(2,4),当a=![]() 时,R(
时,R(![]() ,
,![]() ).
).
【解析】
(1)由题意可求A(-2,0),B(4,0),将A点代入y=ax2-2ax+4,即可求a的值;
(2)设R(t,﹣![]() t2+t+4),过点R作x、y轴的垂线,垂足分别为R',R',可得四边形RR'OR'是矩形,求出S△OCR=
t2+t+4),过点R作x、y轴的垂线,垂足分别为R',R',可得四边形RR'OR'是矩形,求出S△OCR=![]() OCRR'=
OCRR'=![]() ×4t=2t,S△ORB=
×4t=2t,S△ORB=![]() OBRR'=
OBRR'=![]() ×4(﹣
×4(﹣![]() t2+t+4)=﹣t2+2t+8,则有S△RBC=S△ORB+S△OCR﹣S△OBC=﹣t2+2t+8+2t﹣
t2+t+4)=﹣t2+2t+8,则有S△RBC=S△ORB+S△OCR﹣S△OBC=﹣t2+2t+8+2t﹣![]() ×4×4=﹣t2+4t;
×4×4=﹣t2+4t;
(3)设EF、PD交于点G',连EG,可证明OP是EG的垂直平分线,过P作KP⊥x轴于K,PW⊥y轴于W,交RT于点H,则四边形PWOK是正方形,设OT=2a,则TK=KB=CW=2﹣a,HT=OK=PW=2+a,可求HS=TS﹣HT=![]() ﹣(2+a)=
﹣(2+a)=![]() ﹣a,又由tan∠HPS=
﹣a,又由tan∠HPS=![]() ,可得
,可得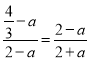 ,则a=1或a=
,则a=1或a=![]() ,即可求R得坐标.
,即可求R得坐标.
解:(1)∵抛物线的对称轴为x=1,AB=6,
∴A(﹣2,0),B(4,0),
将点A代入y=ax2﹣2ax+4,则有0=4a+4a+4,
∴a=﹣![]() ,
,
∴y=﹣![]() x2+x+4;
x2+x+4;
(2)
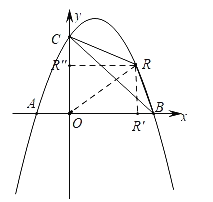
设R(t,﹣![]() t2+t+4),
t2+t+4),
过点R作x、y轴的垂线,垂足分别为R',R',
则∠RR'O=∠RR'O=∠R'OR'=90°,
∴四边形RR'OR'是矩形,
∴RR'=OR'=t,OR'=RR'=﹣![]() t2+t+4,
t2+t+4,
∴S△OCR=![]() OCRR'=
OCRR'=![]() ×4t=2t,
×4t=2t,
S△ORB=![]() OBRR'=
OBRR'=![]() ×4(﹣
×4(﹣![]() t2+t+4)=﹣t2+2t+8,
t2+t+4)=﹣t2+2t+8,
∴S△RBC=S△ORB+S△OCR﹣S△OBC=﹣t2+2t+8+2t﹣![]() ×4×4=﹣t2+4t;
×4×4=﹣t2+4t;
(3)
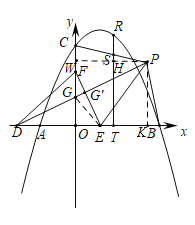
设EF、PD交于点G',连EG,
∵PD⊥EF,
∴∠FG'G=∠DG'E=90°=∠DOG,
∴∠OFE=∠GDO,
∵∠DGO=∠FOE=90°,EF=DG,
∴OP是EG的垂直平分线,
∴OP平分∠COB,
过P作KP⊥x轴于K,PW⊥y轴于W,交RT于点H,
则PW=PK,∠PWO=∠PKO=∠WOK=90°,
∴四边形PWOK是正方形,
∴WO=OK,
∵OC=OB=4,
∴CW=KB,
∵P在BT垂直平分线上,
∴PT=PB,
∴TK=KB=CW,
设OT=2a,则TK=KB=CW=2﹣a,
HT=OK=PW=2+a,
∵OB﹣TS=![]() ,
,
∴HS=TS﹣HT=![]() ﹣(2+a
﹣(2+a![]() ﹣a,
﹣a,
∵tan∠HPS=![]() ,
,
∴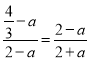 ,
,
∴a=1或a=![]() ,
,
当a=1时,OT=2,∴R(2,4),
当a=![]() 时,OT=
时,OT=![]() ,∴R(
,∴R(![]() ,
,![]() )
)
综上,点R的坐标是(2,4),(![]() ,
,![]() ).
).


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() (k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C,若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
(k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C,若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
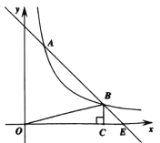
(1)求反比例函数、一次函数的表达式及直线AB与x轴交点E的坐标;
(2)已知点D(t,0)(t>0),过点D作垂直于x轴的直线,在第一象限内与一次函数y=-x+b的图像相交于点P,与反比函数![]() 上的图像相交于点Q,若点P位于点Q的上方,请结合函数图像直接写出此时t的取值范围.
上的图像相交于点Q,若点P位于点Q的上方,请结合函数图像直接写出此时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列8×8的网格中,横、纵坐标均为整点的数叫做格点,△ABC的顶点的坐标分别为A(3,0)、B(0,4)、C(4,2).
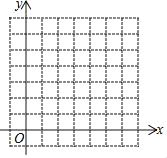
(1)直接写出△ABC的形状;
(2)要求在下图中仅用无刻度的直尺作图:将△ABC绕点B逆时针旋转角度2α得到△A1BC1,其中α=∠ABC,A、C的对应点分别为A1、C1,请你完成作图;
(3)在网格中找一个格点G,使得C1G⊥AB,并直接写出G点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
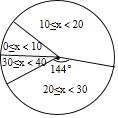
【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组学过锐角三角函数后,到市龙源湖公园测量塑像“夸父追日”的高度,如图所示,在A处测得塑像顶部D的仰角为45°,塑像底部E的仰角为30.1°,再沿AC方向前进10m到达B处,测得塑像顶部D的仰角为59.1°.求塑像“夸父追日”DE高度.(结果精确到0.1m.参考数据:sin30.1°≈0.50,cos30.1°≈0.87,tan30.1°≈0.58,sin59.1°≈0.86,cos59.1°≈0.51,tan59.1°≈1.67)

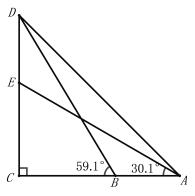
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格纸中,![]() 、
、![]() 都是格点,以
都是格点,以![]() 为圆心,
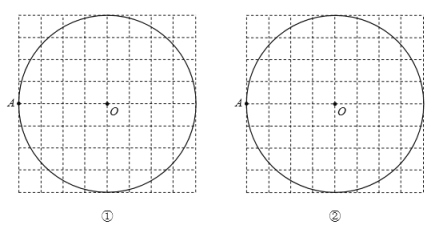
为圆心,![]() 为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
(1)在圆①中画圆![]() 的一个内接正六边形
的一个内接正六边形![]() ;
;
(2)在图②中画圆![]() 的一个内接正八边形
的一个内接正八边形![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O.若BO=6,PO=2,则AP的长,AO的长分别为__________.
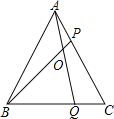
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com