
【题目】如图1,在平面直角坐标系中,等腰![]() 的斜边OB在x轴上,直线
的斜边OB在x轴上,直线![]() 经过等腰
经过等腰![]() 的直角顶点A,交y轴于C点,双曲线
的直角顶点A,交y轴于C点,双曲线![]() 也经过A点
也经过A点![]() 连接BC.
连接BC.
![]() 求k的值;
求k的值;
![]() 判断
判断![]() 的形状,并求出它的面积.
的形状,并求出它的面积.
![]() 若点P为x正半轴上一动点,在点A的右侧的双曲线上是否存在一点M,使得
若点P为x正半轴上一动点,在点A的右侧的双曲线上是否存在一点M,使得![]() 是以点A为直角顶点的等腰直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.
是以点A为直角顶点的等腰直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() 是直角三角形,S△ABC=8;
是直角三角形,S△ABC=8;
(3)在双曲线上存在一点![]() ,使得
,使得![]() 是以点A为直角顶点的等腰三角形.
是以点A为直角顶点的等腰三角形.
【解析】
(1)过点A分别作![]() 轴于M点,
轴于M点,![]() 轴于N点,根据直角三角形的性质可设点A的坐标为
轴于N点,根据直角三角形的性质可设点A的坐标为![]() ,因为点A在直线
,因为点A在直线![]() 上,即把A点坐标代入解析式即可算出a的值,进而得到A点坐标,然后再利用待定系数法求出反比例函数解析式;
上,即把A点坐标代入解析式即可算出a的值,进而得到A点坐标,然后再利用待定系数法求出反比例函数解析式;
(2)利用勾股定理逆定理即可判断出三角形ABC是直角三角形,再利用三角形面积公式求解即可;
(3)由“边角边”易证![]() ≌
≌![]() ,得出
,得出![]() ,那么
,那么![]() 是所求的等腰直角三角形,再根据全等三角形的性质及函数图象与点的坐标的关系得出结果.
是所求的等腰直角三角形,再根据全等三角形的性质及函数图象与点的坐标的关系得出结果.
解:![]() 如图1,
如图1,

过点A分别作![]() 轴于Q点,
轴于Q点,![]() 轴于N点,
轴于N点,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
设点A的坐标为![]() ,
,
![]() 点A在直线
点A在直线![]() 上,
上,
![]() ,
,
解得![]() ,
,
则点A的坐标为![]() ,
,
![]() 双曲线
双曲线![]() 也经过A点,
也经过A点,
![]() ;
;
![]() 由
由![]() 知,
知,![]() ,
,
![]() ,
,
![]() 直线
直线![]() 与y轴的交点为C,
与y轴的交点为C,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 是直角三角形;
是直角三角形;
则S△ABC=![]() AB·BC=
AB·BC=![]() ;
;
![]() 如图2,
如图2,

假设双曲线上存在一点M,使得![]() 是等腰直角三角形;
是等腰直角三角形;
![]() ,
,![]() ,
,
连接AM,BM,
由![]() 知,
知,![]() ,
,
![]() 反比例函数解析式为
反比例函数解析式为![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() 点M的横坐标为4,
点M的横坐标为4,
![]() ;
;
即:在双曲线上存在一点![]() ,使得
,使得![]() 是以点A为直角顶点的等腰三角形.
是以点A为直角顶点的等腰三角形.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过点P(2,﹣3).
(1)求该函数的解析式;
(2)若将点P沿x轴负方向平移3个单位,再沿y轴方向平移n(n>0)个单位得到点P′,使点P′恰好在该函数的图象上,求n的值和点P沿y轴平移的方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则下列四个结论:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中结论正确的序号为( )

A.①②③B.①②C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=120°,∠B=40°,如果过点A的一条直线l把△ABC分割成两个等腰三角形,直线l与BC交于点D,那么∠ADC的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=24,D是BC的中点,AC的垂直平分线EF分别交AC、AD于点E、F,EF = 5 .

(1)求点F到边AB的距离FG的长;
(2)求 F到B点的距离FB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
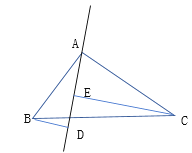
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD![]() DE于点D, CE
DE于点D, CE![]() DE 于点 E.
DE 于点 E.
(1)若BC在DE的同侧(如图所示),且AD=CE,求证:![]()

(2)若B、C在的两侧(如图所示 ),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com