
分析 根据互为相反数两数之和为0列出关系式,利用非负数的性质求出x与y的值,原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x与y的值代入计算即可求出值.
解答 解:∵|x-2+$\sqrt{3}$|与$\sqrt{y-2-\sqrt{3}}$互为相反数,
∴|x-2+$\sqrt{3}$|+$\sqrt{y-2-\sqrt{3}}$=0,
∴x=2-$\sqrt{3}$,y=2+$\sqrt{3}$,
∴原式=[$\frac{(x+y)(x-y)}{(x-y)^{2}}$-$\frac{x}{x-y}$]•$\frac{x(x-y)}{{y}^{2}}$=$\frac{y}{x-y}$•$\frac{x(x-y)}{{y}^{2}}$=$\frac{x}{y}$=$\frac{2-\sqrt{3}}{2+\sqrt{3}}$=7-4$\sqrt{3}$.
点评 此题考查了分式的化简求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
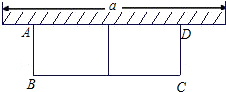 如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).
如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
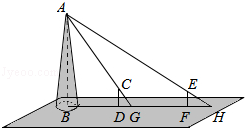 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
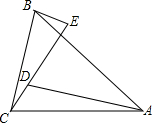 如图,AC=BC,∠CAD=∠BCE,∠ACB=80°,∠E=100°.
如图,AC=BC,∠CAD=∠BCE,∠ACB=80°,∠E=100°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com