
【题目】今年5月14日川航3U863航班挡风玻璃在高空爆裂,机组临危不乱,果断应对.正确处置,顺利返航,避免了一场灾难的发生,下面表格是成都当日海拔高度h(千米)与相应高度处汽温t(℃)的关系(成都地处四川盆地,海拔高度较低,为方便计算,在此题中近似为0米).
海拔高度h(千米) | 0 | 1 | 2 | 3 | 4 | 5 | … |
气温t(℃) | 20 | 14 | 8 | 2 | -4 | -1 | … |
根据上表,回答以下问题:
(1)由上表可知海拔5千米的上空气温约为______℃;
(2)由表格中的规律请写出当日气温t与海拔高度h的关系式为______.
如图是当日飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用的时间关系图.根据图象回答以下问题:
(3)挡风玻璃在高空爆裂时飞机所处的高度为______千米,返回地面用了______分钟;
(4)飞机在2千米高空水平面上大约盘旋了______分钟;
(5)挡风玻璃在高空爆裂时,当时飞机所处高空的气温为______℃,由此可见机长在高空经历了多大的艰险.

【答案】(1)-1 (2)t=20-6h (3)9.8,20 (4)2 (5)-38.8
【解析】
![]() 由表中数据即可得;
由表中数据即可得;![]() 由海拔高度每上升1千米,气温下降
由海拔高度每上升1千米,气温下降![]() 求解可得;
求解可得;![]() 由
由![]() 时
时![]() 及
及![]() 时
时![]() 解答可得;
解答可得;![]() 由函数图象中
由函数图象中![]() 至
至![]() 时,
时,![]() 求解可得;
求解可得;![]() 将
将![]() 代入
代入![]() 求解可得.
求解可得.
解:(1)由上表可知海拔5千米的上空气温约为-1℃,
故答案为:-1;
(2)由表知海拔高度每上升1千米,气温下降6℃,
所以当日气温t与海拔高度h的关系式为t=20-6h,
故答案为:t=20-6h.
(3)由函数图象知挡风玻璃在高空爆裂时飞机所处的高度为9.8千米,返回地面用了20分钟,
故答案为:9.8、20;
(4)飞机在2千米高空水平面上大约盘旋了2分钟,
故答案为:2;
(5)当h=9.8时,t=20-6×9.8=-38.8(℃),
故答案为:-38.8.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
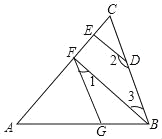
【题目】如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,求证:∠AGF=∠ABC.
试将下面的证明过程补充完整(填空):
证明:∵DE⊥AC,BF⊥AC(已知)
∴∠AFB=∠AED=90°(_______)
∴BF∥DE(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠1=______,(同角的补角相等)
∴GF∥_____(内错角相等,两直线平行),
∴∠AGF=∠ABC.(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某地,人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的竟是关系:

(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)在当地温度![]() 每增加
每增加![]() ,这种蟋蟀
,这种蟋蟀![]() 叫的次数
叫的次数![]() 是怎样变化的?
是怎样变化的?
(3)这种蟋蟀![]() 叫的次数
叫的次数![]() (次)与当地温度
(次)与当地温度![]() 之间的关系为 ;
之间的关系为 ;
(4)当这种蟋蟀![]() 叫的次数
叫的次数![]() 时,求当时该地的温度.
时,求当时该地的温度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连结BD.
(1)若AB=3,BC=4,求边BD的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.

(1)该顾客最少可得_________元购物券,最多可得_________元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分14分)在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
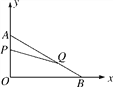
(1)求直线AB的解析式;
(2)当t为何值时,以点A、P、Q为顶点的三角形与△AOB相似?
(3)当t=2秒时,四边形OPQB的面积为多少个平方单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com