
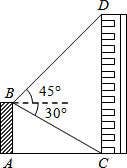
 如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度($\sqrt{3}$=1.7).
如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度($\sqrt{3}$=1.7). 分析 首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.
解答 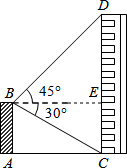 解:如图,过点B作BE⊥CD于点E,
解:如图,过点B作BE⊥CD于点E,
根据题意,∠DBE=45°,∠CBE=30°.
∵AB⊥AC,CD⊥AC,
∴四边形ABEC为矩形.
∴CE=AB=12m.
在Rt△CBE中,cot∠CBE=$\frac{BE}{CE}$,
∴BE=CE•cot30°=12×$\sqrt{3}$=12$\sqrt{3}$.
在Rt△BDE中,由∠DBE=45°,
得DE=BE=12$\sqrt{3}$.
∴CD=CE+DE=12($\sqrt{3}$+1)≈32.4.
答:楼房CD的高度约为32.4m.
点评 考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
 中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 20 | 0.10 |
| 70≤x<80 | 30 | b |
| 80≤x<90 | a | 0.30 |
| 90≤x≤100 | 80 | 0.40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.4(1+x)=4.5 | B. | 1.4(1+2x)=4.5 | ||
| C. | 1.4(1+x)2=4.5 | D. | 1.4(1+x)+1.4(1+x)2=4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com