
【题目】将一副三角板放在同一平面内,使直角顶点重合于点O
(1)如图①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度数.
(2)如图①,你发现∠AOD与∠BOC的大小有何关系?∠AOB与∠DOC有何关系?直接写出你发现的结论.
(3)如图②,当△AOC与△BOD没有重合部分时,(2)中你发现的结论是否还仍然成立,请说明理由.

科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,DF是
,DF是![]() 的中位线,点C关于DF的对称点为E,以DE,EF为邻边构造矩形DEFG,DG交BC于点H,连结CG.
的中位线,点C关于DF的对称点为E,以DE,EF为邻边构造矩形DEFG,DG交BC于点H,连结CG.
![]() 求证:
求证:![]() ≌
≌![]() .
.
![]() 若
若![]() .
.
![]() 求CG的长.
求CG的长.
![]() 在
在![]() 的边上取一点P,在矩形DEFG的边上取一点Q,若以P,Q,C,G为顶点的四边形是平行四边形,求出所有满足条件的平行四边形的面积.
的边上取一点P,在矩形DEFG的边上取一点Q,若以P,Q,C,G为顶点的四边形是平行四边形,求出所有满足条件的平行四边形的面积.
![]() 在
在![]() 内取一点O,使四边形AOHD是平行四边形,连结OA,OB,OC,直接写出
内取一点O,使四边形AOHD是平行四边形,连结OA,OB,OC,直接写出![]() ,
,![]() ,
,![]() 的面积之比.
的面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( ) 
A.AG=BG
B.AB∥EF
C.AD∥BC
D.∠ABC=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕,若EA′恰好平分∠FEB,求∠FEB的度数.
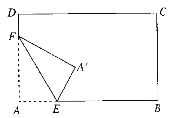
(2)如图,A地和B地都是海上观测站,从A地发现它的北偏东60方向有一艘船P,同时,从B地发现这艘船P在它北偏东30方向.试在图中画出这艘船P的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s). 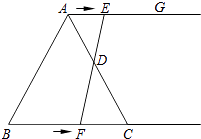
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空: ①当t为s时,四边形ACFE是菱形;
②当t为s时,以A、F、C、E为顶点的四边形是直角梯形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题
![]() 求表中a的值;
求表中a的值;![]() 频数分布直方图补充完整;
频数分布直方图补充完整;
![]() 小亮想根据此直方图绘制一个扇形统计图,请你帮他算出成绩为
小亮想根据此直方图绘制一个扇形统计图,请你帮他算出成绩为![]() 这一组所对应的扇形的圆心角的度数;
这一组所对应的扇形的圆心角的度数;
![]() 若测试成绩不低于80分为优秀,则本次测试的优秀率
若测试成绩不低于80分为优秀,则本次测试的优秀率![]() 百分比
百分比![]() 是多少?
是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
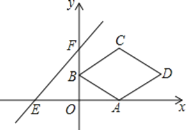
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点C在第一象限,对角线BD与x轴平行
,点C在第一象限,对角线BD与x轴平行![]() 直线
直线![]() 与x轴、y轴分别交于点E,
与x轴、y轴分别交于点E,![]() 将菱形ABCD沿x轴向左平移m个单位,当点D落在
将菱形ABCD沿x轴向左平移m个单位,当点D落在![]() 的内部时
的内部时![]() 不包括三角形的边
不包括三角形的边![]() ,m的值可能是
,m的值可能是![]()
![]()
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半小时后返回A地.如图是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象. 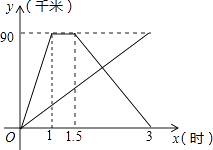
(1)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:![]() ;
;![]() ;
;![]() ;
;![]() ,从中任选两个条件,能使四边形ABCD为平行四边形的选法有
,从中任选两个条件,能使四边形ABCD为平行四边形的选法有![]()
![]()
A. 2种 B. 3种 C. 4种 D. 5种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com