【题目】四边形ABCD中，对角线AC，BD相交于点O，给出下列四个条件：
；
；
；
，从中任选两个条件，能使四边形ABCD为平行四边形的选法有
A. 2种 B. 3种 C. 4种 D. 5种
科目：初中数学 来源： 题型：
【题目】将一副三角板放在同一平面内，使直角顶点重合于点O
（1）如图①，若∠AOB=155°，求∠AOD、∠BOC、∠DOC的度数.
（2）如图①，你发现∠AOD与∠BOC的大小有何关系？∠AOB与∠DOC有何关系？直接写出你发现的结论.
（3）如图②，当△AOC与△BOD没有重合部分时，（2）中你发现的结论是否还仍然成立，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将一朵小花放置在平面直角坐标系中第三象限内的甲位置，先将它绕原点O旋转180°到乙位置，再将它向下平移2个单位长到丙位置，则小花顶点A在丙位置中的对应点A′的坐标为（ ）
A.（3，1）
B.（1，3）
C.（3，﹣1）
D.（1，1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A，B在数轴上对应的数分别为a，b，且|a＋4|＋(b－2)2＝0，点A，B之间的距离记作AB.
(1)线段AB的长为 ；(直接写出结果)
(2)若动点P在数轴上对应的数为x.
①当PA＋PB的值最小时，则奇数x的值为 ；(直接写出结果)
②当PA＋PB＝14时，求x的值；
(3)当动点P在点A的左侧，M，N分别是PA，PB的中点，当点P在A的左侧移动时，聪明的小明同学在计算PM＋PN和PN－PM的值时发现：其中只有一个的值是不变的，请你判断出哪一个的值不变，并求这个值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】完成下面的解题过程，并在括号内填上依据.如图，EF∥AD,∠1=∠2,∠BAC=85°.求∠AGD的度数
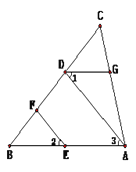
解： ∵EF∥AD,
∴∠2=____( )
又∵∠1=∠2
∴∠1=∠3
∴ ∥____( )
∴∠BAC+____=180°
∵∠BAC=85°
∴∠AGD=950
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从﹣3，﹣1，1，3这五个数中，随机抽取一个数，记为a，若数a使关于x的不等式组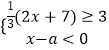 
无解，且使关于x的分式方程 
=﹣1有整数解，那么这5个数中所有满足条件的a的值之和是（ ）
A.﹣2
B.﹣3
C.- 
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在求1＋3＋32＋33＋34＋35＋36＋37＋38的值时，李敏发现：从第二个加数起每一个加数都是前一个加数的3倍，于是她假设：S＝1＋3＋32＋33＋34＋35＋36＋37＋38①，
然后在①式的两边都乘3，得3S＝3＋32＋33＋34＋35＋36＋37＋38＋39②
②－①得，3S－S＝39－1，即2S＝39－1，
所以S＝
.
得出答案后，爱动脑筋的张红想：如果把“3”换成字母a(a≠0且a≠1)，能否求出1＋a＋a2＋a3＋a4＋…＋a2 017的值？如能求出，其正确答案是__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校七年级共有500名学生，团委准备调查他们对“低碳”知识的了解程度，
（1）在确定调查方式时，团委设计了以下三种方案：
方案一：调查七年级部分女生；
方案二：调查七年级部分男生；
方案三：到七年级每个班去随机调查一定数量的学生
请问其中最具有代表性的一个方案是 ；
（2）团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图（如图①、图②所示），请你根据图中信息，将其补充完整；
（3）请你估计该校七年级约有多少名学生比较了解“低碳”知识．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
