
【题目】如图 1,在平面直角坐标系中,图形 W在坐标轴上的投影长度定义如下:设点 P(![]() ,
, ![]() ) ,Q(
) ,Q(![]() ,
, ![]() ) 是图形 W 上的任意两点,若
) 是图形 W 上的任意两点,若![]() 的最大值为 m ,则
的最大值为 m ,则
图形 W 在 x 轴上的投影长度为 lx m ;若![]() 的最大值为 n ,则图形 W 在 y 轴上的
的最大值为 n ,则图形 W 在 y 轴上的
投影长度为 ly n .如图 1,图形 W 在 x 轴上的投影长度为 lx ![]() 4 ;在 y 轴上的 投影长度为 ly
4 ;在 y 轴上的 投影长度为 ly ![]() 3 .
3 .
(1)已知点 A(1, 2) , B(2, 3) , C (3,1) ,如图 2 所示,若图形 W 为四边形 OABC ,
则 lx , ly ;
(2)已知点 C (![]() , 0) ,点 D 在直线 y
, 0) ,点 D 在直线 y ![]() x 1(x 0) 上,若图形 W 为 OCD ,当 lx ly
x 1(x 0) 上,若图形 W 为 OCD ,当 lx ly
时,求点 D 的坐标;
(3 )若图形 W 为函数 y x 2(a x b) 的图象,其中 (0 a b) ,当该图形满足
lx ly 1时,请直接写出 a 的取值范围.
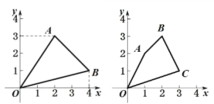
图 1 图 2
【答案】(1)4,3;(2)(-![]() ,
,![]() )或(-10,-14);(3)
)或(-10,-14);(3) ![]() .
.
【解析】
(1)确定出点A在y轴的投影的坐标、点B在x轴上投影的坐标,于是可求得问题的答案;
(2)过点P作PD⊥x轴,垂足为P.设D(x,2x+6),则PD=|2x+6|.PC=|3-x|,然后依据lx=ly,列方程求解即可;
(3)设A(a,a2)、B(b,b2).分别求得图形在y轴和x轴上的投影,由lx=ly可得到b+a=1,然后根据0≤a<b可求得a的取值范围.
解:(1)∵A(3,3),
∴点A在y轴上的正投影的坐标为(0,3).
∴△OAB在y轴上的投影长度ly=3.
∵B(4,1),
∴点B在x轴上的正投影的坐标为(4,0).
∴△OAB在x轴上的投影长度lx=4.
故答案为:4;3.
(2)如图1所示;过点P作PD⊥x轴,垂足为P.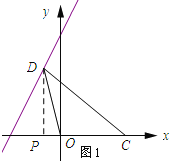
设D(x,2x+6),则PD=2x+6.
∵PD⊥x轴,
∴P(x,0).
∴PC=4-x.
∵lx=ly,
∴2x+6=4-x,解得;x=-![]() .
.
∴D(-![]() ,
,![]() ).
).
如图2所示:过点D作DP⊥x轴,垂足为P.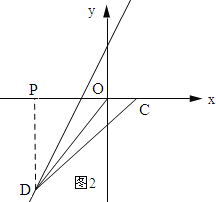
设D(x,2x+6),则PD=-2x-6.
∵PD⊥x轴,
∴P(x,0).
∴PC=4-x.
∵lx=ly,
∴-2x-6=4-x,解得;x=-10.
∴D(-10,-14).
综上所述,点D的坐标为(-![]() ,
,![]() )或(-10,-14).
)或(-10,-14).
(3)如图3所示: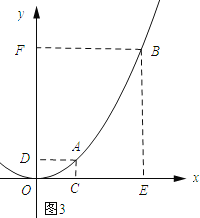
设A(a,a2)、B(b,b2).则CE=b-a,DF=b2-a2=(b+a)(b-a).
∵lx=ly,
∴(b+a)(b-a)=b-a,即(b+a-1)(b-a)=0.
∵b≠a,
∴b+a=1.
又∵0≤a<b,
∴a+a<1,
∴0≤a<![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )

A、3.25m B、4.25m C、4.45m D、4.75m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示A、B、C三点在格点上.

(1)作出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于y对称的△A2B2C2,并写出点C2的坐标.
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司的甲.乙两辆货车分别从A.B两地同时相向而行,并以各自的速度匀速行驶,途径配货站C,甲车先到达C地,并在C地用1小时配货,然后按原速度开往B地,乙车从B地直达A地,如图是甲.乙两车间的距离![]() (千米)与乙车出发
(千米)与乙车出发![]() (时)的函数图像
(时)的函数图像
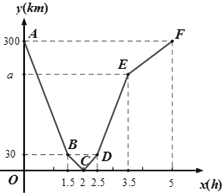
(1)A.B两地的距离是_____千米;
(2)甲车出发______小时到达C地;
(3)坐标系中a的值为________千米;
(4)乙车出发多长时间,两车相距150千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上,请按要求画图和填空:
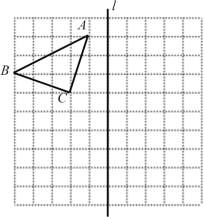
(1)在网格中画出△ABC向下平移5个单位得到的△A1B1C1;
(2)在网格中画出△A1B1C1关于直线l对称的△A2B2C2;
(3)在网格中画出将△ABC绕点A按逆时针方向旋转90度得到的△AB3C3;
(4)在图中探究并求得△ABC的面积= (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边的其中一边的对角对应相等”的情形进行研究.
(初步思考)
我们不妨将问题用符号语言表示为:在△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
(深入探究)
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据______,可以知道Rt△ABC≌Rt△DEF.
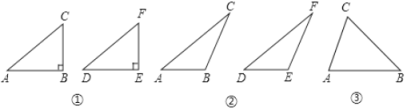
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角.求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角.请你用直尺在图③中作出△DEF,使△DEF和△ABC不全等,并作简要说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.

(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
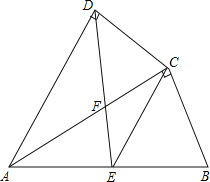
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夹在两条平行线间的正方形ABCD、等边三角形DEF如图所示,顶点A、F分别在两条平行线上.若A、D、F在一条直线上,则∠1与∠2的数量关系是( )
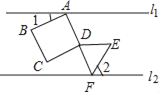
A. ∠1+∠2=60° B. ∠2﹣∠1=30° C. ∠1=2∠2. D. ∠1+2∠2=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com