
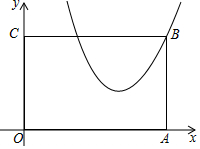
 矩形OABC在平面直角坐标系内的位置如图所示,点O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,点B的坐标为(5,4).将矩形OABC沿某直线1对折,使点B落在坐标轴上的点F处,且BF与1的交点Q恰好落在过点B的抛物线y=x2+mx+14上,则点F的坐标为(1,0)或(3,0)或(0,$\frac{3}{2}$).
矩形OABC在平面直角坐标系内的位置如图所示,点O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,点B的坐标为(5,4).将矩形OABC沿某直线1对折,使点B落在坐标轴上的点F处,且BF与1的交点Q恰好落在过点B的抛物线y=x2+mx+14上,则点F的坐标为(1,0)或(3,0)或(0,$\frac{3}{2}$). 分析 本题要分两种情况进行讨论:
①当F在x轴上时,过Q作x轴的垂线,那么不难得出Q点的纵坐标为AB的一半即为2,然后将其代入抛物线的解析式中即可求出Q点的坐标,然后根据三角形的中位线定理即可求得AM,进而求得AF,即可求得F的坐标.
②当F在y轴上时,过Q作x轴的垂线,那么不难得出Q点的横坐标为OA的一半即为2.5,然后将其代入抛物线的解析式中即可求出Q点的坐标,然后根据梯形的中位线定理即可求得OF,即可求得F的坐标.
解答 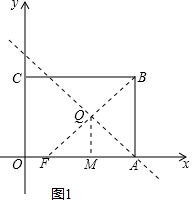 解:∵点B的抛物线y=x2+mx+14上,点B的坐标为(5,4).
解:∵点B的抛物线y=x2+mx+14上,点B的坐标为(5,4).
∴4=25+5m+14,
解得m=-7,
∴抛物线的解析式为y=x2-7x+14,
①当点F在x轴上时,过Q作QM⊥x轴于M,
由题意可知QM=$\frac{1}{2}$AB=2,则Q点的纵坐标为2,
代入y=x2-7x+14得,x2-7x+14=2,
∴x=3或x=4
∴Q点的坐标为(3,2)或(4,2),
当Q点坐标为(3,2)时,如图1,OM=3,MA=2,FA=4,
∴F(1,0);
当Q点坐标为(4,2)时,如图1,OM=4,MA=1,FA=2,
∴F(3,0);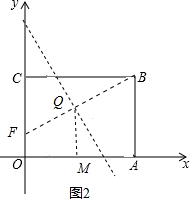
②当点F在y轴上时,由题意可知OM=$\frac{1}{2}$OA=$\frac{5}{2}$,则Q点的横坐标为$\frac{5}{2}$,
代入y=x2-7x+14得,y=$\frac{25}{4}$-$\frac{35}{2}$+14=$\frac{11}{4}$,
∴Q点的坐标为($\frac{5}{2}$,$\frac{11}{4}$),
∴QM=$\frac{11}{4}$,
∵QM=$\frac{1}{2}$(OF+AB),
∴OF=2QM-AB=2×$\frac{11}{4}$-4=$\frac{3}{2}$,
∴F(0,$\frac{3}{2}$);
综上,点F的坐标为(1,0)或(3,0)或(0,$\frac{3}{2}$);
故答案为(1,0)或(3,0)或(0,$\frac{3}{2}$).
点评 本题着重考查了矩形的性质、图形翻折变换、中位线定理以及一次函数和二次函数的相关知识等重要知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.


科目:初中数学 来源: 题型:选择题
| A. | y=x2-2 | B. | y=x2+2 | C. | y=(x+3)2+2 | D. | y=(x-3)2-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | -1 | 2 | 3 | 2 | … |
| A. | y1>y2 | B. | y1≤y2 | C. | y1<y2 | D. | y1≥y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com