Question

【题目】如图，冬生、夏亮两位同学从学校出发到青年路小学参加现场作为比赛，冬生步行一段时间后，夏亮骑自行车沿相同路线行进，两人都是匀速前进，他们的路程差s（米）与冬生出发时间t（分）之间的函数关系如图所示．

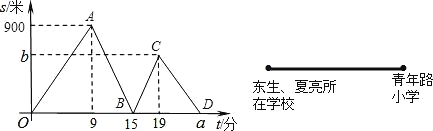
根据图象进行以下探究：

（1）冬生的速度是 米/分，请你解释点B坐标（15，0）所表示的意义： ；

（2）求夏亮的速度和他们所在学校与青年路小学的距离；

（3）求a，b值及线段CD所表示的y与x之间的函数关系，并写出自变量的取值范围．

Answer 1

【答案】（1）100，冬生出发15分时，夏亮追上冬生；（2）2500米；

（3）y=﹣100x+2500（19≤x≤25）．

【解析】

试题分析：（1）由图象可知，0～8分时为冬生步行，根据速度=路程÷时间求出冬生的速度；点B所表示的意义：冬生出发15分时，夏亮追上冬生；

（2）根据15分时，夏亮追上冬生，利用追击问题的等量关系求出夏亮的速度，再根据路程=速度×时间列式计算即可夏亮运动的距离，即他们所在学校与青年路小学的距离；

（3）根据路程=速度×时间列式计算即可求出a、b，最后根据待定系数法即可求得线段CD所表示的y与x之间的函数关系．

试题解析：（1）冬生的速度：900÷9=100米/分，

点B所表示的意义：冬生出发15分时，夏亮追上冬生；

故答案为：100，冬生出发15分时，夏亮追上冬生；

（2）当冬生出发15分时，夏亮运动了15﹣9=6（分），运动的距离是：15×100=1500（米），

∴夏亮的速度：1500÷6=250（米/分），

当第19分以后两人距离越来越近，说明夏亮已到达终点，故夏亮先到达青年路小学，此时夏亮运动的时间为19﹣9=10（分），运动的距离为10×250=2500（米），

故他们所在学校与青年路小学的距离是2500米；

（3）由（1）（2）可知，两所学校相距2500米，冬生的速度是100米/分，

故a==25，b=100×（25﹣19）=600，

设线段CD所表示的y与x之间的函数关系为y=kx+b，由题意得

，解得．

故y=﹣100x+2500（19≤x≤25）．