
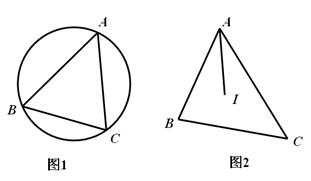
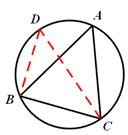
 。
。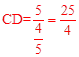 。
。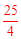 。
。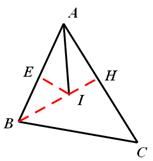
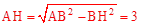 。
。 ,∴
,∴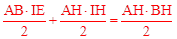 ,即
,即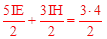 。
。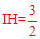 。
。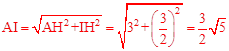 。
。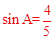 ,根据锐角三角函数定义即可求得△ABC外接圆的直径。
,根据锐角三角函数定义即可求得△ABC外接圆的直径。 求得
求得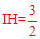 。在Rt△AIH中,应用勾股定理求得AI的长。
。在Rt△AIH中,应用勾股定理求得AI的长。

 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源:不详 题型:解答题
 ,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
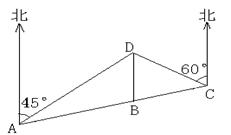
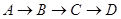 的线路输送天然气,某测绘员测得D市在A市东北方向,在B市正北方向,在C市北偏西
的线路输送天然气,某测绘员测得D市在A市东北方向,在B市正北方向,在C市北偏西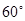 方向。C市在A市北偏东
方向。C市在A市北偏东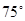 方向。B、D两市相距20km,问天然气从A市输送到D市的路程是多少?(结果保留整数,参考数据:
方向。B、D两市相距20km,问天然气从A市输送到D市的路程是多少?(结果保留整数,参考数据: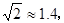
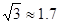 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
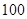 米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为
米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为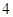 秒且∠APO=60°,∠BPO =45°.
秒且∠APO=60°,∠BPO =45°. 
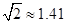 ,
,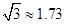 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com