
 ,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
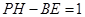 ,证明见解析
,证明见解析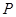 作
作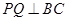 于
于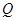
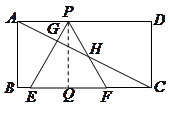
 矩形
矩形
 ,即
,即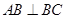 ,又
,又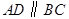
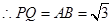 ………………1分
………………1分 是等边三角形
是等边三角形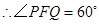
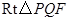 中
中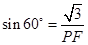
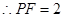
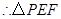 的边长为
的边长为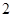 . ……………………………3分
. ……………………………3分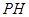 与
与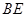 的数量关系是:
的数量关系是: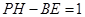 ………4分
………4分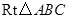 中,
中,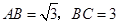
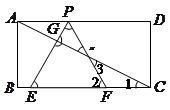
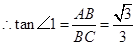
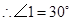 …………………………………5分
…………………………………5分 是等边三角形
是等边三角形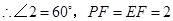 ……………………………6分
……………………………6分
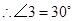
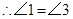
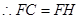 …………………………………………8分
…………………………………………8分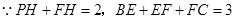
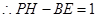 ……………………………………………9分
……………………………………………9分

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源:不详 题型:解答题
 .如图,把△ABC的一边BC放置在x轴上,有OB=14,OC=
.如图,把△ABC的一边BC放置在x轴上,有OB=14,OC= ,AC与y轴交于点E.
,AC与y轴交于点E.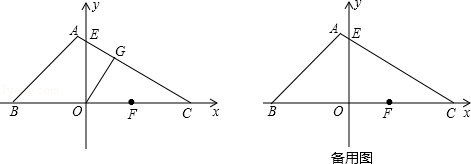
查看答案和解析>>
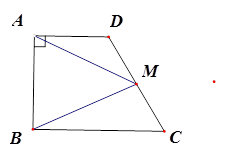
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
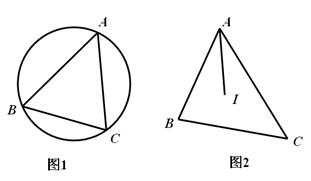
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
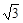 ≈1.732,结果保留整数).
≈1.732,结果保留整数).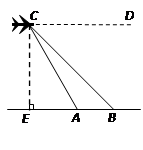
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
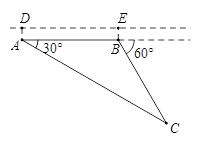
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com