
【题目】如图1,正方形ABCD中,点E、F分别在边DC、AD上,且AE⊥BF于G. 
(1)求证:BF=AE;
(2)如图2,当点E在DC延长线上,点F在AD延长线上时,(1)中结论是否成立?(直接写结论) 
(3)在图2中,若点M、N、P、Q分别为四边形AFEB四条边AF、EF、EB、AB的中点,且AF:AD=4:3,求S四边形MNPQ:S正方形ABCD .
【答案】
(1)
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ADC=90°.
∴∠DAE+∠BAE=90°.
∵AE⊥BF,
∴∠AGB=90°,
∴∠GAB+∠GBA=90°,
∴∠DAE=∠ABG.
在△ABF和△DAE中,
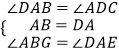 ,
,
∴△ABF≌△DAE(ASA),
∴BF=AE;
(2)
解:)结论成立 即AE=BF.
理由:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ADC=90°.
∴∠DAE+∠BAE=90°.
∵AE⊥BF,
∴∠AGB=90°,
∴∠GAB+∠GBA=90°,
∴∠DAE=∠ABG.
在△ABF和△DAE中,
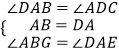 ,
,
∴△ABF≌△DAE(ASA),
∴BF=AE;
(3)
解:∵AF:AD=4:3,设AF=4a,AD=3a,
∴DF=a.
∵△ABF≌△DAE,
∴AF=DE,
∴AF﹣AD=DE﹣DC,
∴DF=CE,
∴CE=a.
∵点M、N、P、Q分别为四边形AFEB四条边AF、EF、EB、AB的中点,
∴MN是△AEF的中位线,MQ是△ABF的中位线,
∴MN= ![]() AE,MN∥AE,MQ=
AE,MN∥AE,MQ= ![]() BF,MQ∥BF.
BF,MQ∥BF.
∴MN=MQ.∠MNP=∠NPQ=∠PQM=90°,
∴四边形MNPQ是正方形.
在Rt△ABF中,由勾股定理,得
BF=5a.
∴MN=MQ= ![]() .
.
∴S四边形MNPQ= ![]() .
.
∵S正方形ABCD=9a2,
∴S四边形MNPQ:S正方形ABCD= ![]() :9a2=25:36.
:9a2=25:36.
答:S四边形MNPQ:S正方形ABCD=25:36.
【解析】(1)根据正方形的性质就可以求出△ABF≌△DAE,就可以得出结论;(2)根据正方形的性质就可以求出△ABF≌△DAE就可以得出BF=AE;(3)根据条件可以设AF=4a,AD=3a,就可以求出DF=CE=a,由勾股定理就可以求出AE,由中位线的性质就可以求出MN的值,表示出正方形MNPQ的面积,就可以求出结论.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形).


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.

(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作 MG⊥EF交线段BC于点G,判断△GEF的形状,并说明理由;
(3)如图3,若AB= ![]() ,过点M作 MG⊥EF交线段BC的延长线于点G.
,过点M作 MG⊥EF交线段BC的延长线于点G.
①直接写出线段AE长度的取值范围;
②判断△GEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(徐州中考)如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长交DC于点F,求证:
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
频数(通话次数) | 20 | 16 | 9 | 5 |
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A. 10% B. 40% C. 50% D. 90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D在边BA或BA的延长线上,过点D作DE∥BC,交∠ABC的角平分线于点E.
(1)如图1,当点D在边BA上时,点E恰好在边AC上,求证:∠ADE=2∠DEB;
(2)如图2,当点D在BA的延长线上时,请直接写出∠ADE与∠DEB之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
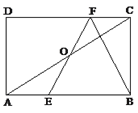
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC。
(1)求证;OE=OF;(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为
中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为![]() ,点B在x负半轴上,反比例函数
,点B在x负半轴上,反比例函数![]() 的图象经过C点.
的图象经过C点.
(1)求该反比例函数的解析式;
(2)当函数值![]() >-2时,请直接写出自变量x的取值范围;
>-2时,请直接写出自变量x的取值范围;
(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长均为1的7×7网格图中,格点上有A,B,C,D,E五个定点,如图所示,一个动点P从点E出发,绕点A逆时针旋转90°,之后该动点继续绕点B,C,D逆时针90°后回到初始位置,点P运转路线的总长是 . (结果保留π)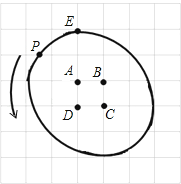
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com