练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，连接AC.若AC=8，则四边形ABCD的面积为（　　）

    A.32B.24C.40D.36

    【答案】A

    【解析】

    作辅助线；证明△ABM≌△ADN，得到AM＝AN，△ABM与△ADN的面积相等；求出正方形AMCN的面积即可解决问题．

    解：如图，作AM⊥BC、AN⊥CD，交CD的延长线于点N；
    ∵∠BAD＝∠BCD＝90°
    ∴四边形AMCN为矩形，∠MAN＝90°；
    ∵∠BAD＝90°，
    ∴∠BAM＝∠DAN；
    在△ABM与△ADN中，

    ∴△ABM≌△ADN（AAS），
    ∴AM＝AN（设为a）；△ABM与△ADN的面积相等；
    ∴四边形ABCD的面积＝正方形AMCN的面积；
    由勾股定理得：AC2＝AM2＋MC2，而AC＝8；
    ∴2a2＝64，a2＝32，
    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：在△ABC和△DCE中，∠ACB=∠DCE=90°，AC=DC，BC=EC，AB与DE相交于点F．

    （1）如图1，求证AB=DE；

    （2）如图2，连接CF，求证∠AFC=∠EFC；

    （3）如图3，在（2）的条件下，当AF=EF时，连接BD，AE，延长CF交BD于点G，AE交CF于点H，若AE=8，BG=2，求线段GH的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，对角线AC与BD相交于点O，点E是BC上的一个动点，连接DE， 交 AC于点F.

    (1)如图①，当时，求的值；

    (2)如图②当DE平分∠CDB时，求证：AF=OA；

    (3)如图③，当点E是BC的中点时，过点F作FG⊥BC于点G，求证：CG=BG.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=mx+1的图象经过点A（﹣1，0），且与反比例函数（k≠0）交于点B（n，2）．

    （1）求一次函数的解析式

    （2）求反比例函数的解析式

    （3）直接写出求当1≤x≤6时，反比例函数y的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中， ， 平分，

    交于点，⊙O是的外接圆．

    （1）求证： 是⊙O的切线；

    （2）若， ，求⊙O的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

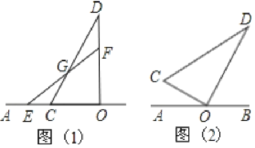
    【题目】如图，已知点O在直线AB上，将一副直角三角板的直角顶点放在点O处，其中∠OCD=60°，∠OEF=45°．边OC、OE在直线AB上．

    （1）如图（1），若CD和EF相交于点G，则∠DGF的度数是______°；

    （2）将图（1）中的三角板OCD绕点O顺时针旋转30°至图（2）位置

    ①若将三角板OEF绕点O顺时针旋转180°，在此过程中，当∠COE=∠EOD=∠DOF时，求∠AOE的度数；

    ②若将三角板OEF绕点O以每秒4°的速度顺时针旋转180°，与此同时，将三角板OCD绕点O以每秒1°的速度顺时针旋转，当三角板OEF旋转到终点位置时，三角板OCD也停止旋转．设旋转时间为t秒，当OD⊥EF时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知菱形ABCD的对角线AC、BD相交于点O，延长AB至点E，使BE＝AB，连接CE．

    （1）求证：四边形BECD是平行四边形；

    （2）若∠E＝60°，AC＝，求菱形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AF∥CD，CB平分∠ACD，BD平分∠EBF，且BC⊥BD，下列结论：① BC平分∠ABE；② AC∥BE；③ ∠CBE+∠D＝90°；④ ∠DEB＝2∠ABC．其中正确结论的个数有（　　）

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数的图象的一支位于第一象限．

    （1）判断该函数图象的另一支所在的象限，并求m的取值范围；

    （2）如图，O为坐标原点，点A在该反比例函数位于第一象限的图象上，点B与点A关于轴对称，若△OAB的面积为6，求m的值．

    查看答案和解析>>

    同步练习册答案