
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 平分
平分![]() ,
,
![]() 交
交![]() 于点
于点![]() ,⊙O是
,⊙O是![]() 的外接圆.
的外接圆.
(1)求证: ![]() 是⊙O的切线;
是⊙O的切线;
(2)若![]() ,
, ![]() ,求⊙O的面积.
,求⊙O的面积.

【答案】(1)证明见解析;(2)⊙O的面积为![]() .
.
【解析】试题分析:(1)连接OE,由于BE是角平分线,则有∠CBE=∠OBE;而OB=OE,就有∠OBE=∠OEB,等量代换有∠OEB=∠CBE,那么利用内错角相等,两直线平行,可得OE∥BC;又∠C=90°,所以∠AEO=90°,即AC是⊙O的切线;
(2)先利用勾股定理可求出半径OD,从而求出圆的面积.
试题解析:解:(1)证明:连接OE .

∵BE平分∠ABC, ∴∠CBE=∠OBE.
又OB=OE,∴∠OEB=∠OBE,∴ ∠CBE=∠OEB, ∴BC∥OE,∴∠OEA=∠C=90°.
又点E在⊙O上, ∴AC是⊙O的切线.
(2)设⊙O的半径为r,∵∠OEA=90°,∴![]() ,
,
即![]() ,解得r=
,解得r=![]() , ∴⊙O的面积S=π×
, ∴⊙O的面积S=π×![]() =
=![]() π.
π.


科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3,用<a>表示大于a的最小整数.例如:<2.5>=3,<4>=5,<-1.5>=-1.解决下列问题:
(1)[-2.6]=______,<6.2>=______.
(2)已知x,y满足方程组 ,则[x]=______,<y>=______,x的取值范围是______,y的取值范围是______.
,则[x]=______,<y>=______,x的取值范围是______,y的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
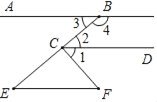
【题目】把下面的推理过程补充完整,并在括号内填上理由.
已知:B、C、E三点在一条直线上,∠3=∠E,∠4+∠2=180°.
试说明:∠BCF=∠E+∠F
解:∵∠3=∠E(已知)
∴EF∥ (内错角相等,两直线平行)
∵∠4+∠2=180°(已知)
∴CD∥
∴CD∥ (平行于同一条直线的两条直线互相平行)
∴∠1=∠F,
∠2=
∵∠BCF=∠1+∠2(已知)
∴∠BCF=∠E+∠F(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生的安全意识,某校组织了一次全校1500名学生都参加的“安全知识”考试,考题共10题.考试结束后,学校随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽查的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题:

(1)本次抽查的样本容量是 ;在扇形统计图中,m= ,n= ,“答对10题”所对应扇形的圆心角为 度;
(2)将条形统计图补充完整;
(3)请根据以上调查结果,估算出该校答对超过7题的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】燃放烟花爆竹是中国春节的传统民俗,可注重低碳、环保、健康的市民让今年的烟花爆竹遇冷.在江北区北滨路一烟花爆竹销售点了解到,某种品牌的烟花2013年除夕每箱进价100元,售价250元,销售量40箱 .而2014年除夕当天和去年当天相比,该店的销售量下降了![]() %(
%(![]() 为正整数),每箱售价提高了
为正整数),每箱售价提高了![]() %,成本增加了50%,其销售利润仅为去年当天利润的50%.则
%,成本增加了50%,其销售利润仅为去年当天利润的50%.则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=8,则四边形ABCD的面积为( )

A.32B.24C.40D.36
查看答案和解析>>
科目:初中数学 来源: 题型:
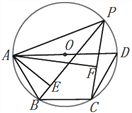
【题目】如图:点P是四边形ABCD外接圆⊙O上的任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD,连接PA,PB,PC,若PA= ![]() ,求点A到PB和PC的距离之和AE+AF是多少?
,求点A到PB和PC的距离之和AE+AF是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=8cm,BC=16cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
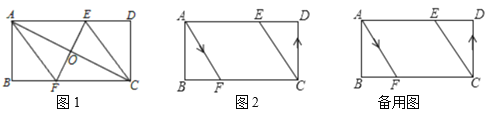
(1)如图1,连接AF、CE,判断四边形AFCE的形状,并说明理由;
(2)如图2,动点P、Q分别从A、C两点同时出发,P点沿着A→F→B→A匀速运动,Q点沿着C→D→E→C匀速运动,在运动过程中:
① 已知点P的速度为10cm/s,点Q的速度为8cm/s,运动时间为t秒,问当t为何值时,点A,C,P,Q组成的四边形为平行四边形?
② 点P,Q的运动路程分别为a,b(单位:cm,ab≠0),问当a,b满足怎样的关系式时,点A,C,P,Q组成的四边形为平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).

(1)求抛物线的解析式;
(2)判断△ABC的形状,直接写出△ABC外接圆的圆心坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com