【题目】下列不能判断四边形ABCD是平行四边形的是（ ）
A. AB=CD，AD=BC B. AB∥CD，AD=BC
C. AB∥CD，AD∥BC D. ∠A=∠C，∠B=∠D
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，点P的坐标为（
，
），点Q的坐标为（
，
），且
，
，若P，Q为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”．下图为点P，Q 的“相关矩形”的示意图．
（1）已知点A的坐标为（1，0）．
①若点B的坐标为（3，1）求点A，B的“相关矩形”的面积；
②点C在直线x=3上，若点A，C的“相关矩形”为正方形，求直线AC的表达式；
（2）⊙O的半径为
，点M的坐标为（m，3）．若在⊙O上存在一点N，使得点M，N的“相关矩形”为正方形，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．
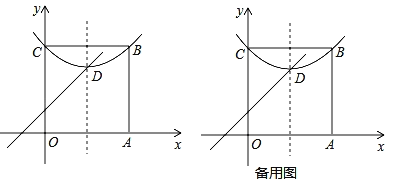
问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线
经过B、C两点，顶点D在正方形内部．
（1）直接写出点D（m，n）所有的特征线；
（2）若点D有一条特征线是y=x+1，求此抛物线的解析式；
（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“重庆到处都人从众”……今年的五一小长假，相信重庆市民的朋友圈已被“重庆太火”刷屏了.据重庆市旅游发展委员会公布的数据显示，五一节四天，重庆共接待境内外游客2559万人次，2259万用科学记数法表示为_______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下面的变形规律：
=1﹣ 
； 
= ﹣ 
； 
= ﹣ 
；…解答下面的问题：
（1）若n为正整数，请你猜想 
=；
（2）求和： + + ．（注：只能用上述结论做才能给分）；
（3）用上述相似的方法求和： 
+ 
+ 
+…+ 
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料并回答问题：
材料1：如果一个三角形的三边长分别为a，b，c，记
，那么三角形的面积为
． ①
古希腊几何学家海伦（Heron，约公元50年），在数学史上以解决几何测量问题而闻名．他在《度量》一书中，给出了公式①和它的证明，这一公式称海伦公式．
我国南宋数学家秦九韶（约1202﹣﹣约1261），曾提出利用三角形的三边求面积的秦九韶公式：
． ②
下面我们对公式②进行变形：
．
这说明海伦公式与秦九韶公式实质上是同一公式，所以我们也称①为海伦﹣﹣秦九韶公式．
问题：如图，在△ABC中，AB=13，BC=12，AC=7，⊙O内切于△ABC，切点分别是D、E、F．
（1）求△ABC的面积；
（2）求⊙O的半径．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
