
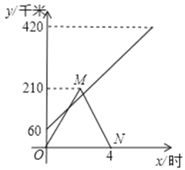
����Ŀ���ס��������ֱ�����420km��A��B����������У��ҳ��ȼ׳��ȳ���1Сʱ�������ֱ��Ը��Ե��ٶ�������ʻ��;��C�أ�A��B��C������ͬһ��ֱ���ϣ����׳�����C�غ�������������ԭ·ԭ�ٷ���A�أ��ҳ���B��ֱ��A�أ��ס�����������Գ����ص�·��y��ǧ�ף���׳���ʻ���õ�ʱ��x��Сʱ���Ĺ�ϵ��ͼ��ʾ�����ͼ����Ϣ�ش��������⣺
��1���׳����ٶ����� ��ǧ��/ʱ���ҳ����ٶ����� ��ǧ��/ʱ��
��2����׳����������ص�·��y��ǧ�ף�������ʻ���õ�ʱ��x��Сʱ��֮��ĺ�����ϵʽ��
��3���׳������ʱ����������90ǧ�ף�����ֱ��д���𰸣�
���𰸡���1��105��60����2��y��![]() ����3��
����3��![]() ʱ��
ʱ��![]() ʱ��
ʱ��![]() ʱ��
ʱ��
��������
��1����������ͺ���ͼ���е����ݿ��Եõ������������ٶȣ�
��2����������ͺ���ͼ���е����ݿ�����ü׳����������ص�·��y��ǧ�ף�������ʻ���õ�ʱ��x��Сʱ��֮��ĺ�����ϵʽ��
��3�����������֪�����������90ǧ������������Ӷ����Խ���⣮
��1����ͼ�ɵã�
�׳����ٶ�Ϊ����210��2����4��420��4��105ǧ��/ʱ��
�ҳ����ٶ�Ϊ��60ǧ��/ʱ��
�ʴ�Ϊ��105��60��
��2����ͼ��֪����M������Ϊ��2��210����
��0��x��2ʱ����y��k1x��
��M��2��210���ڸú���ͼ���ϣ�
2k1��210��
��ã�k1��105��
��y��105x��0��x��2����
��2��x��4ʱ����y��k2x+b��
��M��2��210���͵�N��4��0���ڸú���ͼ���ϣ�
��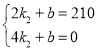 ����
����![]() ��
��
��y����105x+420��2��x��4����
�����������׳����������ص�·��y����������ʱ��x�ĺ�����ϵʽΪ��y��![]() ��
��
��3����׳�����aСʱʱ�������90ǧ�ף�
���״�A�ص�C��ʱ��
105a+60��a+1��+90��420��
��ã�a��![]() ��
��
���״�C�ط���A��ʱ��
��210��60��3��+��105��60������a��2����90��
��ã�a��![]() ��
��
������A�غ�
420��60��a+1����90��
��ã�a��![]() ��
��
�𣺼׳�����![]() ʱ��
ʱ��![]() ʱ��
ʱ��![]() ʱ���������90ǧ�ף�
ʱ���������90ǧ�ף�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=120��������ABC�Ƶ�A˳ʱ����תһ���Ƕȣ�С��360�����õ���B��AC�䣮
��1������B�������߶�AC�ϣ���ͼ�л�����B��AC������ֱ��д����AC=4ʱ��CC����ֵ��
��2������ACB=20������ת��B��C����AC����ֱ��д����ת�ǵĶ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A(![]() ,0),AB��
,0),AB��![]() ��,��AB=10,��C��0��b��,
��,��AB=10,��C��0��b��,![]() ,b����
,b����![]() .��P��t,0�����߶�AO��һ�㣨������A,O��
.��P��t,0�����߶�AO��һ�㣨������A,O��
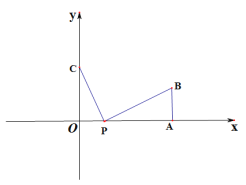
��1����t=5ʱ����PB��PC��ֵ��
��2����PC+PB��Сʱ����t��ֵ;
��3����������ϵ������������������:����m,n����m+n=10,������![]() =
=![]() ��������
��������![]() ����Сֵ=________.
����Сֵ=________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ������������ε�������������AB��A'B'��ֱ��ͶӰ��P��AB��A'B'�ϵĸ����ڽ���ƽ����ͶӰ��������֪CD��ͶӰ��Ϊ2 cm��CC'��ͶӰ��Ϊ6 cm.
(1)������������ͶӰ��P�ϵ���ͶӰ;
(2)����������ı����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴ٽ�ѧ����������չ��ijУ��֯��չ�����Ż���ֱ������������ࡢ�����ࡢ��ѧ�༰���������ţ�Ҫ�����˲������ţ�ÿ��ֻ��ѡ��һ���Ϊ�˽�ѧ��ϲ���������Ż��ѧУ����һ�γ������飮�����ռ��������ݣ����Ƴ�����������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺

��1���˴ι������˶����ˣ�
��2������ѧ����������ͳ��ͼ����ռԲ�ĽǵĶ�����
��3���뽫����ͳ��ͼ����������
��4������У��1500��ѧ���������ϲ�����������ŵ�ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
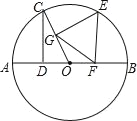
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ڡ�O�ϣ�CD��AB��D���ҡ�COD=60�㣬EΪ��BC��һ���㣨�����B��C�غϣ�����E�ֱ�����EF��AB��F��EG��OC��G���ָ��������ĸ����⣺
�١�GEF=60�㣻��CD=GF���ۡ�GEFһ��Ϊ���������Σ���E�ڻ�BC���˶�ʱ������ij��ʱ��ʹ����GEFΪ�ȱ������Σ�
������ȷ��������_____����д��������ȷ�������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
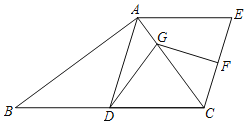
����Ŀ����ͼ����Rt��ABC�У�ADΪб��BC�ϵ����ߣ�AE��BC��CE��AD��EC�Ĵ�ֱƽ����FG��AC��G������DG������ADG��24�������B�Ķ���Ϊ_____�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ƽ��ֱ������ϵ�У�B��C���������ֱ�ΪB��0��3����C��0����![]() ������A��x���������ϣ��������BAO��30����
������A��x���������ϣ��������BAO��30����
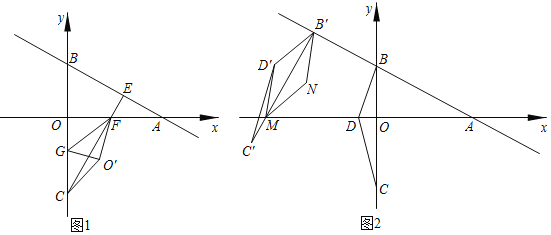
��1������C��CE��AB�ڵ�E����AO�ڵ�F����GΪ�߶�OC��һ���㣬����GF������OFG��FG����ʹ��O����ƽ���ڵĵ�O����������O��C�����߶�OF�ij��Լ��߶�O��C����Сֵ��
��2����ͼ2����D������ΪD����1��0��������BDC�Ƶ�B˳ʱ����ת��ʹ��BC��AB�ڵ�B������ת�����BDC��ֱ��ABƽ�ƣ�ƽ���е���BDC��Ϊ��B��D��C������ֱ��B��C����x�ύ�ڵ�M��NΪƽ��������һ�㣬����B����D����M��NΪ������ı���������ʱ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
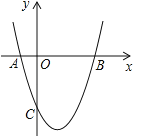
����Ŀ����ͼ��������y=x2+bx+c��x�ύ��A����1��0����B��3��0�����㣬��![]() �ύ��
�ύ��![]() �㣮
�㣮
��1����������ߵĽ���ʽ��
��2��P��y����������һ�㣬�ҡ�PAB����ABΪ���ĵ��������Σ������P�����ꣻ
��3����ֱ��BC������Q��ֱ��BC�·��������ϵ�һ���㣬������QBC����Ƿ������ֵ�����У��������ʱQ������ꣻ��û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com