
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求□ABCD的面积.

【答案】(1)证明见解析(2)32
【解析】试题分析:(1)根据平行四边形的性质,可证DF∥EB,然后根据一组对边平行且相等的四边形为平行四边形可证四边形DEBF是平行四边形,然后根据有一个角是直角的平行四边形是矩形可证;
(2)根据(1)可知DE=BF,然后根据勾股定理可求AD的长,然后根据角平分线的性质和平行线的性质可求得DF=AD,然后可求CD的长,最后可用平行四边形的面积公式可求解.
试题解析:(1)∵四边形ABCD是平行四边形,
∴DC∥AB,即DF∥EB.
又∵DF=BE,
∴四边形DEBF是平行四边形.
∵DE⊥AB,
∴∠EDB=90°.
∴四边形DEBF是矩形.
(2)∵四边形DEBF是矩形,
∴DE=BF=4,BD=DF.
∵DE⊥AB,
∴AD=![]() =
=![]() =5.
=5.
∵DC∥AB,
∴∠DFA=∠FAB.
∵AF平分∠DAB,
∴∠DAF=∠FAB.
∴∠DAF=∠DFA.
∴DF=AD=5.
∴BE=5.
∴AB=AE+BE=3+5=8.
∴S□ABCD=AB·BF=8×4=32.


科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.
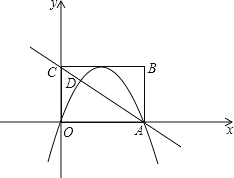
(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:
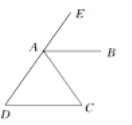
(1)∵________=__________(已知)
∴AB∥CD(同位角相等,两条直线平行)
(2)∵_________=__________(已知)
∴AB∥CD(内位角相等,两条直线平行)
(3)∵_________+_________=180(已知)
∴AB∥CD(同旁内角互补,两条直线平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
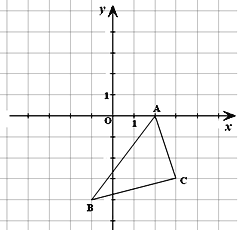
【题目】如图所示的直角坐标系中,解答下列问题:
(1)分别写出A、B两点的坐标;
(2)将△ABC向左平移3个单位长度,再向上平移5个单位长度,画出平移后的△A1B1C1;
(3)求 △A1B1C1的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com