
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.
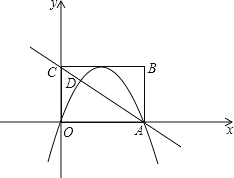
(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
【答案】(1)y=-![]() x2+3x;(2) 点D坐标为(1,
x2+3x;(2) 点D坐标为(1,![]() );(3)存在,N1(2,0),N2(6,0),N3(-
);(3)存在,N1(2,0),N2(6,0),N3(-![]() -1,0),N4(
-1,0),N4(![]() -1,0).
-1,0).
【解析】
试题分析:(1)由OA的长度确定出A的坐标,再利用对称性得到顶点坐标,设出抛物线的顶点形式y=a(x-2)2+3,将A的坐标代入求出a的值,即可确定出抛物线解析式;
(2)设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,确定出直线AC解析式,与抛物线解析式联立即可求出D的坐标;
(3)存在,分两种情况考虑:如图所示,当四边形ADMN为平行四边形时,DM∥AN,DM=AN,由对称性得到M(3,![]() ),即DM=2,故AN=2,根据OA+AN求出ON的长,即可确定出N的坐标;当四边形ADM′N′为平行四边形,可得三角形ADQ全等于三角形N′M′P,M′P=DQ=
),即DM=2,故AN=2,根据OA+AN求出ON的长,即可确定出N的坐标;当四边形ADM′N′为平行四边形,可得三角形ADQ全等于三角形N′M′P,M′P=DQ=![]() ,N′P=AQ=3,将y=-
,N′P=AQ=3,将y=-![]() 代入得:-
代入得:-![]() =-
=-![]() x2+3x,求出x的值,确定出OP的长,由OP+PN′求出ON′的长即可确定出N′坐标.
x2+3x,求出x的值,确定出OP的长,由OP+PN′求出ON′的长即可确定出N′坐标.
试题解析:(1)设抛物线顶点为E,根据题意OA=4,OC=3,得:E(2,3),
设抛物线解析式为y=a(x-2)2+3,
将A(4,0)坐标代入得:0=4a+3,即a=-![]() ,
,
则抛物线解析式为y=-![]() (x-2)2+3=-
(x-2)2+3=-![]() x2+3x;
x2+3x;
(2)设直线AC解析式为y=kx+b(k≠0),
将A(4,0)与C(0,3)代入得:![]() ,
,
解得: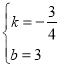 ,
,
故直线AC解析式为y=-![]() x+3,
x+3,
与抛物线解析式联立得: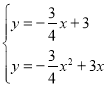 ,
,
解得:![]() 或
或![]() ,
,
则点D坐标为(1,![]() );
);
(3)存在,分两种情况考虑:
①当点M在x轴上方时,如图1所示:
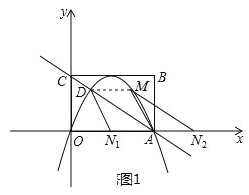
四边形ADMN为平行四边形,DM∥AN,DM=AN,
由对称性得到M(3,![]() ),即DM=2,故AN=2,
),即DM=2,故AN=2,
∴N1(2,0),N2(6,0);
②当点M在x轴下方时,如图2所示:
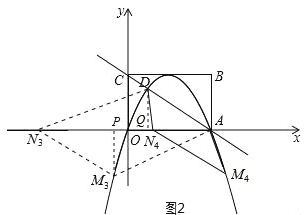
过点D作DQ⊥x轴于点Q,过点M作MP⊥x轴于点P,可得△ADQ≌△NMP,
∴MP=DQ=![]() ,NP=AQ=3,
,NP=AQ=3,
将yM=-![]() 代入抛物线解析式得:-
代入抛物线解析式得:-![]() =-
=-![]() x2+3x,
x2+3x,
解得:xM=2-![]() 或xM=2+
或xM=2+![]() ,
,
∴xN=xM-3=-![]() -1或
-1或![]() -1,
-1,
∴N3(-![]() -1,0),N4(
-1,0),N4(![]() -1,0).
-1,0).
综上所述,满足条件的点N有四个:N1(2,0),N2(6,0),N3(-![]() -1,0),N4(
-1,0),N4(![]() -1,0).
-1,0).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,AH是边BC上的高.
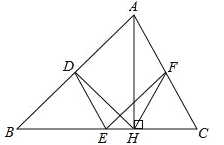
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=﹣![]() x+3交AB,BC分别于点M,N,反比例函数y=
x+3交AB,BC分别于点M,N,反比例函数y=![]() 的图象经过点M,N.
的图象经过点M,N.
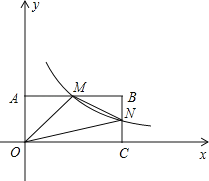
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
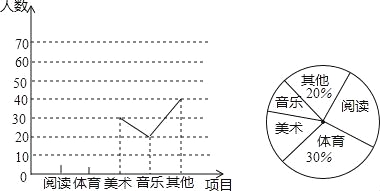
【题目】某学校为了解该校学生的课余活动情况,抽样调查了部分同学,将所得数据处理后,制成折线统计图(部分)和扇形统计图(部分)如下:
(1)在这次研究中,一共调查了 名学生.
(2)补全频数分布折线图;
(3)该校共有2200名学生,估计该校学生中爱好阅读的人数大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求□ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
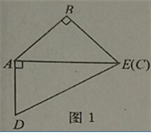
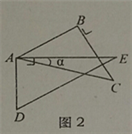
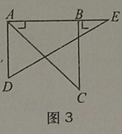
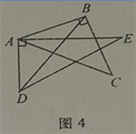
【题目】如图,取一副三角板按图1拼接,固定三角板ADE(含30°),将三角板ABC(含45°)绕点A顺时针方向旋转一个大小为α的角(0°<α≤45°),试问:
(1)当∠α=_____度时,能使图2中的AB∥DE;
(2)当旋转到AB与AE重叠时(如图3),则∠α=_____度;
(3)当△ADE的一边与△ABC的某一边平行(不共线)时,直接写出旋转角α的所有可能的度数;
(4)当0°<α≤45°时,连接BD(如图4),探求∠DBC+∠CAE+∠BDE的值的大小变化情况,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com