
【题目】在△ABC中,AB=AC,点D在直线BC上(不与点B、C重合),线段AD绕A点逆时针方向旋转∠BAC的大小,得线段AE,连接DE、CE.探索∠BCE与∠BAC的大小关系,并加以证明.

【答案】见解析.
【解析】
分类讨论:
当点D在线段BC上,如图1,根据旋转的性质得AD=AE,再由∠DAE=∠BAC得到∠BAD=∠CAE,则可根据SAS判定△ABD≌△ACE,得到∠ABC=∠ACE,而∠BCE=∠BCA+∠ACE=∠BCA+∠ABC,而∠BAC+∠BCA+∠ABC=180°,于是得到∠BCE+∠BAC=180°;
当点D再BC的延长线上,如图2,同样可证明△ABD≌△ACE,得到∠ABD=∠ACE,同样可得∠BCE+∠BAC=180°;
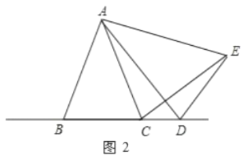
当点D再CB延长线上时,如图3,同样可证明△ABD≌△ACE,得到∠ABD=∠ACE,根据三角形外角性质得∠ABD=∠BAC+∠ACB,∠ACE=∠ACB+∠BCE,所以∠BCE=∠BAC;
综上所述,∠BCE与∠BAC相等或互补.
∠BCE与∠BAC相等或互补.
理由如下:
当点D在线段BC上,如图1,
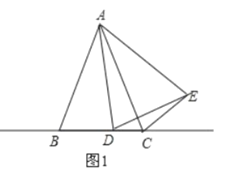
∵线段AD绕点A按逆时针方向旋转得到AE
∴AD=AE
∵∠DAE=∠BAC
∴∠BAD=∠CAE
在△ABD和△ACE中
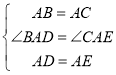
∴△ABD≌△ACE(SAS)
∴∠ABC=ACE
∴∠BCE=∠BCA+∠ACE=∠BCA+∠ABC
∵∠BAC+∠BCA+∠ABC=180°
∴∠BCE+∠BAC=180°
当点D再BC的延长线上,如图2,
同样可证明△ABD≌△ACE,得到∠ABD=ACE
同样得到∠BCE+∠BAC=180°
当点D再CB延长线上时,如图3,
同样可证明△ABD≌△ACE,得到∠ABD=ACE
∵∠ABD=∠BAC+∠ACB
∠ACE=∠ACB+∠BCE
∴∠BCE=∠BAC
综上所述,∠BCE与∠BAC相等或互补.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFl,得到图②.
(1)在图①中,过点P作PM∥AB,当α=20°,β=50°时,∠EPM= 度,∠EPF= 度;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请直接写出α与β的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0 (a≠0)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,方程x2-6x+8=0的两个根是2和4,则方程x2-6x+8=0就是“倍根方程”.
(1)若一元二次方程x2-3x+c=0是“倍根方程”,则c= ;
(2)若(x-2) (mx-n)=0(m≠0)是“倍根方程”,求代数式4m2-5mn+n2的值;
(3)若方程ax2+bx+c=0 (a≠0)是倍根方程,且相异两点M(1+t,s),N(4-t,s),都在抛物线y=ax2+bx+c上,求一元二次方程ax2+bx+c=0 (a≠0)的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
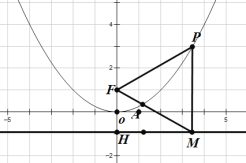
【题目】二次函数图象的顶点在原点O,经过点A(1,![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M.
求证:![]() PFM为等腰三角形;
PFM为等腰三角形;
(3)作PQ![]() FM于点Q,当点P从横坐标2013处运动到横坐标2017处时,请求出点Q运动的路径长.
FM于点Q,当点P从横坐标2013处运动到横坐标2017处时,请求出点Q运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,四边形ABCD中,AB=7,BC=3,∠ABC=∠ACD=∠ADC=45°,求BD的长;
(2)如图2,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学六七年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠DAC的度数为( )

A. 90° B. 80° C. 70° D. 60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com