
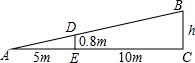
 如图所示,小亮在打网球时,网高0.8m,网到拍的水平距离为10m,为使球恰好能打过网,而且落在离网5m位置上,求球拍击球的高度h.
如图所示,小亮在打网球时,网高0.8m,网到拍的水平距离为10m,为使球恰好能打过网,而且落在离网5m位置上,求球拍击球的高度h.  高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:选择题
| A. | 5.7112×1012元 | B. | 5.7112×1011元 | C. | 5.7112×1010元 | D. | 5.7112×109元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
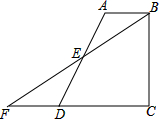 如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
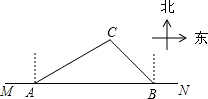 2009年3月21日邵阳市荣获“省卫生城市称号”,在创卫过程中,要在东西方向M、N两地之间修建一条道路,已知:如图,C点周围180米范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500米到达B处,测得C在B的北偏西45°方向上,问MN是否穿过文物保护区?为什么?
2009年3月21日邵阳市荣获“省卫生城市称号”,在创卫过程中,要在东西方向M、N两地之间修建一条道路,已知:如图,C点周围180米范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500米到达B处,测得C在B的北偏西45°方向上,问MN是否穿过文物保护区?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com