
| x | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |
分析 (1)利用待定系数法求出一次函数解析式,进而得出答案;
(2)利用(1)中所求解析式进而得出平均每天的修建费.
解答 解:(1)设y关于x的函数解析式为:y=kx+b,
则$\left\{\begin{array}{l}{50k+b=40}\\{60k+b=38}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{5}}\\{b=50}\end{array}\right.$,
故y关于x的函数解析式为:y=-$\frac{1}{5}$x+50;
(2)由(1)得:y=-$\frac{1}{5}$×40+50=42(万元),
答:平均每天的修建费是42万元.
点评 此题主要考查了一次函数的应用,利用待定系数法求出一次函数解析式是解题关键.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:选择题
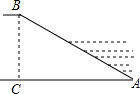 如图所示,河堤横断面迎水坡AB的坡比是1:2,堤高BC=5m,则坡面AB的长度是
如图所示,河堤横断面迎水坡AB的坡比是1:2,堤高BC=5m,则坡面AB的长度是| A. | 10m | B. | 10$\sqrt{5}$m | C. | 15m | D. | 5$\sqrt{5}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com