
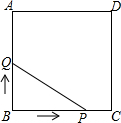
 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )| A. | 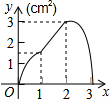 | B. | 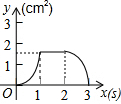 | C. | 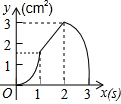 | D. | 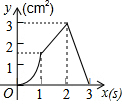 |
分析 首先根据正方形的边长与动点P、Q的速度可知动点Q始终在AB边上,而动点P可以在BC边、CD边、AD边上,再分三种情况进行讨论:①0≤x≤1;②1<x≤2;③2<x≤3;分别求出y关于x的函数解析式,然后根据函数的图象与性质即可求解.
解答 解:由题意可得BQ=x.
①0≤x≤1时,P点在BC边上,BP=3x,
则△BPQ的面积=$\frac{1}{2}$BP•BQ,
解y=$\frac{1}{2}$•3x•x=$\frac{3}{2}$x2;故A选项错误;
②1<x≤2时,P点在CD边上,
则△BPQ的面积=$\frac{1}{2}$BQ•BC,
解y=$\frac{1}{2}$•x•3=$\frac{3}{2}$x;故B选项错误;
③2<x≤3时,P点在AD边上,AP=9-3x,
则△BPQ的面积=$\frac{1}{2}$AP•BQ,
解y=$\frac{1}{2}$•(9-3x)•x=$\frac{9}{2}$x-$\frac{3}{2}$x2;故D选项错误.
故选:C.
点评 本题考查了动点问题的函数图象,正方形的性质,三角形的面积,利用数形结合、分类讨论是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 射线(不含端点) | B. | 线段(不含端点) | C. | 直线 | D. | 抛物线的一部分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
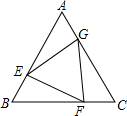 如图,已知正△ABC的边长为2,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
如图,已知正△ABC的边长为2,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )| A. | 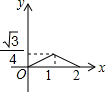 | B. | 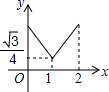 | C. | 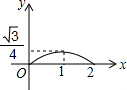 | D. | 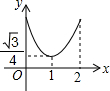 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
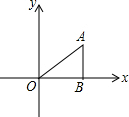 如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为( )
如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为( )| A. | (-1,$\sqrt{3}$) | B. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | C. | (-1,-$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$)或(-$\sqrt{3}$,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于5π.
如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于5π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
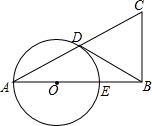 已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com