
分析 (1)直接利用概率公式计算;
(2)画树状图展示所有12种等可能的结果数,再根据坐标轴上点的坐标特征,找出点(x,y)位于坐标轴上的结果数.然后根据概率公式求解.
解答 解:(1)从中任取一球,该球上标记的数字为负数的概率=$\frac{2}{4}$=$\frac{1}{2}$;
(2)画树状图为: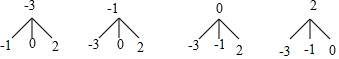
共有12种等可能的结果数,其中点(x,y)位于坐标轴上的结果数为6,
所以点(x,y)位于坐标轴上的概率=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
| 老师1 | 老师2 | 老师3 | 老师4 | 老师5 | |
| 李璐 | 90 | 92 | 94 | 95 | 88 |
| 王润 | 89 | 86 | 87 | 94 | 91 |
| “好”票数 | “较好”票数 | “一般”票数 | |
| 李璐 | 40 | 7 | 3 |
| 王润 | 42 | 4 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
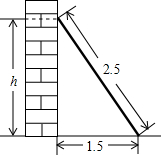 如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m.
如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com