
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,AB=5.点P从点A出发,以每秒5个单位
长度的速度沿AC方向运动,过点P作PQ⊥AB于点Q,当点Q和点B重合时,点P停止运动,以AP和AQ为边作APHQ.设点P的运动时间为t秒(t>0)
(1)线段PQ的长为 .(用含t的代数式表示)
(2)当点H落在边BC上时,求t的值.
(3)当APHQ与△ABC的重叠部分图形为四边形时,设四边形的面积为S,求S与t之间的函数关系式.
(4)过点C作直线CD⊥AB于点D,当直线CD将APHQ分成两部分图形的面积比为1:7时,直接写出t的值.

【答案】(1)4t;(2)t=![]() ;(3)当0<t≤
;(3)当0<t≤![]() 时, S=12t2,当
时, S=12t2,当![]() ≤t≤
≤t≤![]() 时,S==﹣
时,S==﹣![]() t2+
t2+![]() t;(4)t的值为
t;(4)t的值为![]() 或
或![]() s.
s.
【解析】
(1)利用勾股定理求出BC,再根据sinA=![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
(2)如图2中,因为QH∥AC,可得![]() ,由此构建方程即可解决问题;
,由此构建方程即可解决问题;
(3)两种情形分别求解:①如图3中,当0<t≤![]() 时,重叠部分是四边形APHQ.②如图4中,当
时,重叠部分是四边形APHQ.②如图4中,当![]() ≤t≤
≤t≤![]() 时,重叠部分是四边形ACMQ;
时,重叠部分是四边形ACMQ;
(4)两种情形画出图形分别利用三角形的中位线定理求解即可;
(1)如图1中,
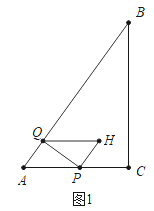
在Rt△ACB中,∵AC=3,AB=5,∠C=90°,
∴BC=![]() =4,
=4,
∵AP=5t,sinA=![]() ,
,
∴![]() ,
,
∴PQ=4t,AQ=![]() =3t.
=3t.
故答案为4t.
(2)如图2中,当点H落在BC上时.
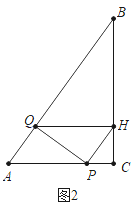
∵QH∥AC,
∴![]() ,
,
∴![]() ,
,
∴t=![]() .
.
(3)①如图3中,当0<t≤![]() 时,重叠部分是四边形APHQ.S=12t2.
时,重叠部分是四边形APHQ.S=12t2.

②如图4中,当![]() ≤t≤
≤t≤![]() 时,重叠部分是四边形ACMQ,
时,重叠部分是四边形ACMQ,
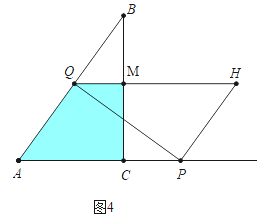
S=![]() =﹣
=﹣![]() t2+
t2+![]() t.
t.
(4)①如图5中,∵S△HEF:S五边形EQAPF=1:7,CD∥PQ,
∴EF是△HPQ的中位线.
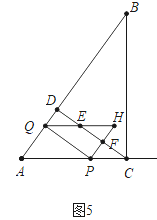
∵cos∠A=![]() ,
,
∴AD=![]() ,
,
∵QH∥AC,
∴∠DQE=∠A,
∴cos∠DQE=cos∠A=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴t=![]() .
.
②如图6中,当S△ADC:S五边形CDQHP=1:7时,CD是△APQ的中位线.
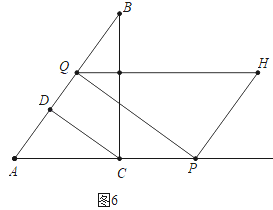
∴AQ=2AD,
∴3t=2×![]() ,
,
∴t=![]() .
.
综上所述,满足条件的t的值为![]() 或
或![]() s.
s.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】某地地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款![]() 元,第三天收到捐款
元,第三天收到捐款![]() 元.
元.
![]() 如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
![]() 按照
按照![]() 中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
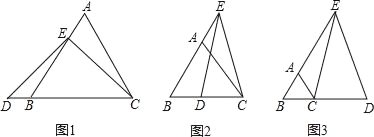
【题目】已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED=EC.
(1)当点E在AB的上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;
(2)当点E在BA的延长线上,点D在BC上时(如图2),猜想AE、AC和CD的数量关系,并证明你的猜想;
(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请直接写出AE、AC和CD的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=110°,点E、G分别是AB、AC的中点,DE⊥AB交BC于D,FG⊥AC交BC于F,连接AD、AF.试求∠DAF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑工程队利用一面墙(墙的长度不限),用40米长的篱笆围成一个长方形的仓库.
(1)求长方形的面积是150平方米,求出长方形两邻边的长;
(2)能否围成面积220平方米的长方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年初,“合肥百大”商场在滨湖新区隆重开业,某服装经销商发现某款新型运动服市场需求较大,该服装的进价为![]() 元/件,每年支付员工工资和场地租金等其它费用总计
元/件,每年支付员工工资和场地租金等其它费用总计![]() 元.经过市场调查发现如果销售单价为
元.经过市场调查发现如果销售单价为![]() 元/件,则年销售量为
元/件,则年销售量为![]() 件.
件.
![]() 用含
用含![]() 的代数式表示年获利金额
的代数式表示年获利金额![]() ;
;
注:年获利![]() (销售单价-进价)
(销售单价-进价)![]() 年销售量-其它费用
年销售量-其它费用
![]() 若经销商希望该服装一年的销售获利达
若经销商希望该服装一年的销售获利达![]() 元,且要使产品销售量较大,你认为销售单价应定为多少元?
元,且要使产品销售量较大,你认为销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
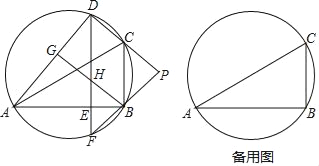
【题目】如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com