练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在圆O中，弦AB为圆内接正六边形的边长，弦AC为圆内接正方形的边长，那么∠BAC=
     
    ．
    考点：正多边形和圆
    专题：
    分析：如图，根据正多边形和圆得出∠OAB=60°，∠OAC=45°，从而得出∠BAC的度数．
    解答：解：如图，
    ∵弦AB为圆内接正六边形的边长，弦AC为圆内接正方形的边长，
    ∴∠OAB=60°，∠OAC=45°，
    ∴∠BAC=∠OAB-∠OAC=60°-45°=15°，
    故答案为15°．
    点评：本题考查了正多边形和圆，计算正多边形的中心角是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    4x2=a，y2=25a，那么x与y的关系是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知一次函数y=-2x+m的图象与x轴和y轴围成的三角形面积为1，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在△ABC和△A′B′C′中，如果∠A=48°，∠C=102°，∠A′=48°，∠B′=30°，那么这两个三角形能否相似的结论是
     
    ，理由是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

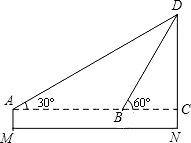    在测量操场旗杆高度的综合实践活动中某小组测绘了如下所示的示意图其中测角仪的高为1.5m，在A处测得旗杆顶部D的倾角为30°，他把测角仪向前搬了10m到达B处后，在此测得旗杆顶部D的仰角为60°，求旗杆DN的高度（结果保留小数点后一位．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

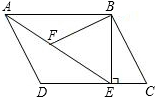    如图，在平行四边形ABCD中，AB=4，BC=3，过点B作BE⊥CD于E，连接AE，∠AEB=60°，F为AE上一点，且∠BFE=∠C．
    （1）求证：△ABF∽△EAD；
    （2）求AE的长；
    （3）求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    七中育才学校为鼓励学生进行微电影拍摄，出台了相关规定：由学校统一给学生提供光碟刻录，学生在教育研讨会期间自主销售，刻录成本价与出厂价之间的差价由学校承担．李明按照规定拍摄了一部质量较高的微电影．已知该部微电影光盘的成本价为每盘10元，刻录商家出厂价为每盘12元，销售量y（盘）与销售单价x（元）之间的关系近似满足一次函数：y=-10x+500．
    （1）李明把销售单价定为20元，那么学校为他承担的总差价为多少元？
    （2）设李明获得的利润为w（元），当销售单价定为多少元时，可获得最大利润？
    （3）学校规定销售单价不得高于25元．如果李明想要获得的利润不低于3000元，那么学校为他承担的总差价最少为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    口袋中有2个红球1个黑球，每次摸后放回，3次都摸到红球的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    因式分解：（ab+b）2-（a+1）2．

    查看答案和解析>>

    同步练习册答案