
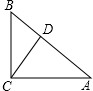
 已知在Rt△ABC中,∠ACB=90°,BC=5,CD⊥AB,AC=12,求:
已知在Rt△ABC中,∠ACB=90°,BC=5,CD⊥AB,AC=12,求:分析 (1)根据勾股定理即可求得AB的长,根据三角形三角函数的计算即可求得sinA的值;
(2)根据△ABC面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,即可求得CD的长;
(3)根据∠ACD=∠B,可求得cos∠ACD的值.
解答 解:(1)在Rt△ABC中,∠ACB=90°,BC=5,AC=12,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,sinA=$\frac{BC}{AB}=\frac{5}{13}$;
(2)∵S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,
∴AB•CD=AC•BC,
∴CD=$\frac{AC•BC}{AB}=\frac{12×5}{13}=\frac{60}{13}$;
(3)∵CD⊥AB,
∴∠B=∠ACD,
∴cos∠ACD=cos∠B=$\frac{CB}{AB}=\frac{5}{13}$.
点评 本题主要考查的是解直角三角形,解答本题需要同学们熟练掌握锐角三角函数的定义和勾股定理,面积法的应用是解题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
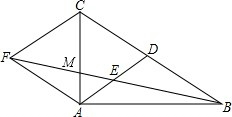 如图,在△ABC中,∠BAC=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,BF交AC于点M,连接CF.
如图,在△ABC中,∠BAC=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,BF交AC于点M,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
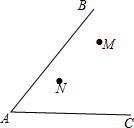 如图,南开中学高二年级的学生分别在五云山寨M,N两处参加社会时间活动.先要在道路AB,AC形成的锐角∠BAC内设一个休息区P,使P到两条道路的距离相等,并且使得PM=PN,请用直尺和圆规作出P点的位置(不写作法,值保留作图痕迹).
如图,南开中学高二年级的学生分别在五云山寨M,N两处参加社会时间活动.先要在道路AB,AC形成的锐角∠BAC内设一个休息区P,使P到两条道路的距离相等,并且使得PM=PN,请用直尺和圆规作出P点的位置(不写作法,值保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{(-2)}^{2}}$=${(-\sqrt{2})}^{2}$ | B. | $\sqrt{{(\sqrt{7}-3)}^{2}}$=$\sqrt{7}$-3 | C. | $\sqrt{{x}^{2}+2x+1}$=x+1 | D. | $\sqrt{{x}^{2}-25}$=$\sqrt{x+5}$•$\sqrt{x-5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com