
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A(![]() ��0)��B(3
��0)��B(3![]() ��2)��C��0��2)������D��ÿ��1����λ���ٶ�
��2)��C��0��2)������D��ÿ��1����λ���ٶ�
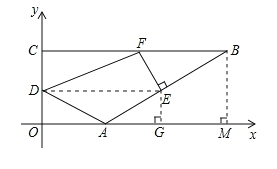
�ӵ�0������OC���յ�C�˶���ͬʱ����E��ÿ��2����λ���ٶȴӵ�A������AB���յ�B�˶�������E��EF��AB����BC�ڵ�F������DA��DF�����˶�ʱ��Ϊt�룮
(1)���ABC�Ķ�����
(2)��tΪ��ֵʱ��AB��DF��
(3)���ı���AEFD�����ΪS��
����S����t�ĺ�����ϵʽ��
����һ������y=x2+mx��������E����S<2![]() ʱ����m��ȡֵ��Χ(д���𰸼���)��
ʱ����m��ȡֵ��Χ(д���𰸼���)��

���𰸡�(1)30o;(2) ![]() ;(3)
;(3) ![]()
![]()
�������������������1�����ABC�Ķ��������BAx�Ķ�������B��BM��x����M����AM=2![]() ��BM=2���ɴ˿ɵó���BAM����ABC�Ķ�����
��BM=2���ɴ˿ɵó���BAM����ABC�Ķ�����
��2����AB��FDʱ����CFD=��B=30�㣬����ֱ��������CDF�У���CD�ij���ʾ��CF��ͬ������ֱ��������FEB�У���BE�ij���ʾ��BF��Ȼ��ɸ���CF+BF=BC�����t��ֵ��
��3��������DE������D��E���ٶȿ�֪AE=2OD����AE=2EG�����OD��=EG�����ı���ODEG�Ǿ��Σ����DE��x�ᣬ��ô�ı���AEFD������ɷֳ�������ADE��������EFD��������������������ζ���DEΪ�ף��������θߵĺ�������OC�ij�������ı���ADEF������͵���![]() DEOC���ؼ������DE�ij��������A��DE�Ĵ��߲��ѵó�DE=OA+AEsin60�㣬�ɴ˿ɵó�S��t�ĺ�����ϵʽ��
DEOC���ؼ������DE�ij��������A��DE�Ĵ��߲��ѵó�DE=OA+AEsin60�㣬�ɴ˿ɵó�S��t�ĺ�����ϵʽ��
����֪��S��ȡֵ��Χ�ɸ��ݢٵĺ�����ϵʽ���t��ȡֵ��Χ���ڢ����Ѿ������E�����꣬������������ߵĽ���ʽ�У���m��ʾ��t��ֵ��Ȼ�����t��ȡֵ��Χ�������m��ȡֵ��Χ��
���������
��1������B��BM��x���ڵ�M
��C��0��2����B��![]() ��
��
��BC��OA
���ABC=��BAM
��BM=2��AM=![]()
��tan��BAM=![]()
���ABC=��BAM=30�㣮
��2����AB��DF
���CFD=��CBA=30��
��Rt��DCF�У�CD=2-t����CFD=30�㣬
��CF=![]() ��2-t��
��2-t��
��AB=4��
��BE=4-2t����FBE=30�㣬
��BF=![]()
��![]()
��t=![]()
��3��������DE������E��EG��x���ڵ�G��
��EG=t��OG=![]() t+
t+![]()
��E(![]() t+
t+![]() ,t)
,t)
��DE��x��
S=S��DEF+S��DEA=![]() DE��CD+
DE��CD+![]() DE��OD
DE��OD
=![]() t+
t+![]()
�ڵ�S��![]() ʱ��
ʱ��
�ɢٿ�֪��S=![]() t+
t+![]()
��![]() t+
t+![]() <
<![]()
��t��1��
��t��0��
��0��t��1��
��y=-x2+mx����E(![]() t+
t+![]() ,t)
,t)
��t=0ʱ��E��![]() ,0��
,0��
��m=![]()
��t=1ʱ��E��![]() ,1��
,1��
��m=![]()
��![]()


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����E��F�ֱ�ΪABCD�ı�BC��AD�ϵĵ㣬�ҡ�1=��2��
��֤��AE=CF��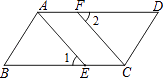
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.3ab-2ab=1
B.x4��x2=x6
C.��x2��3=x5
D.3x2��x=2x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��y���������ϣ���B���C����x���ϣ��ҵ�B�ڵ�C����࣬����BC=OA������3am��1b2��anb2n��2��ͬ������OA=m��OB=n�����m��n��ֵ�Լ���C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����β�����ֱ����ԼΪ0.000000101������0.000000101�ÿ�ѧ������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У������ж�����ֱ��������ȫ�ȵ����� ��
A��һ����Ǻ�б�߶�Ӧ���
B������ֱ�DZ߶�Ӧ���
C��������Ƕ�Ӧ���
D��б�ߺ�һ��ֱ�DZ߶�Ӧ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A��2����2����B����1����2������ֱ��AB��x���y���λ�ù�ϵ�ֱ��ǣ� ��
A.�ཻ���ཻ
B.ƽ�У�ƽ��
C.ƽ�У���ֱ�ཻ
D.��ֱ�ཻ��ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȫ��ͼ�ε���״��ͬ����С��ȣ���ȫ�������εĶ�Ӧ����ȣ���ȫ�������ε��ܳ�������ֱ���ȣ��������ȵ�����������ȫ�ȣ�������ȷ��˵��Ϊ��������
A. �٢ۢ� B. �ڢۢ� C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=�� ![]() x+2��y=2x��3��ͼ��ֱ�y����A��B���㣬����һ�κ�����ͼ���ཻ�ڵ�P��
x+2��y=2x��3��ͼ��ֱ�y����A��B���㣬����һ�κ�����ͼ���ཻ�ڵ�P��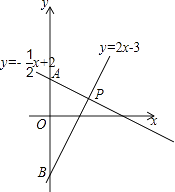
��1�����PAB�������
��2����֤����APB=90�㣻
��3������һ�κ���y=2x��3��ͼ������һ��N���Һ�����Ϊx������NA����ֱ��д����NAP���������x�ĺ�����ϵʽ����д����Ӧx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com