
【题目】如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中结论一定正确的序号数是( )
.其中结论一定正确的序号数是( )

A. ①② B. ①③ C. ③④ D ②④
【答案】B
【解析】①由于∠A=60°;在△ABC中,∠ABC+∠ACB=180°-∠A=120°,即∠FBC+∠FCB=60°,而∠BFE正好是△BFC的外角,即∠BFE=∠FBC+∠FCB=60°所以![]() ,故正确;
,故正确;
②若BC=BD,需满足一个条件:∠BCD=∠BDC,且看这两个角的表达式:∠BCD=180°-∠A-2∠DBA=120°-2∠DBA;∠BDC=∠BDA+∠A=60°+∠DBA;联立两式,可得∠DBA=20°;此时∠ABC=40°,而没有任何条件可以说明∠ABC的度数是40°,即可得出本选项错误.
③由于F是∠ABC和∠ACB角平分线的交点,因此F是△ABC的内心,可过F作AB、AC的垂线,通过证构建的直角三角形全等,得出FE=FD的结论,因结论正确;
④若BF=2DF,则F是△ABC的重心,即三边中线的交点,而题目给出的条件是F是△ABC的内心,显然两者的结论相矛盾,因此不正确.
所以本题正确的结论:①③.
故选B.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,点P的坐标为( ![]() ),点Q的坐标为
),点Q的坐标为 ![]() ,且
,且 ![]() ,
, ![]() ,若P,Q为某个矩形的两个顶点,且该矩形的一组对边与某条坐标轴平行,则称该矩形为点P,Q的“相关矩形”,图2及图3中点A的坐标为(4,3).
,若P,Q为某个矩形的两个顶点,且该矩形的一组对边与某条坐标轴平行,则称该矩形为点P,Q的“相关矩形”,图2及图3中点A的坐标为(4,3).
(1)若点B的坐标为(-2,0),则点A,B的“相关矩形”的面积为;
(2)点C在y轴上,若点A,C的“相关矩形”的面积为8,求直线AC的解析式;
(3)如图3,直线 ![]() 与x轴交于点M,与y轴交于点N,在直线MN上是否存在点D,使点A,D的“相关矩形”为正方形,如果存在,请求出点D的坐标,如果不存在,请说明理由.
与x轴交于点M,与y轴交于点N,在直线MN上是否存在点D,使点A,D的“相关矩形”为正方形,如果存在,请求出点D的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,线段AC=8,BC=6,点M、N分别是AC、BC的中点.
(1)求MN的长度;
(2)根据(1)的计算过程与结果,设AC+BC=a,其它条件不变,你能猜想出MN的长度吗?请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=72°,∠C=30°,①求∠BAE的度数;②求∠DAE的度数;
(2)探究:如果只知道∠B=∠C+42°,也能求出∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示: 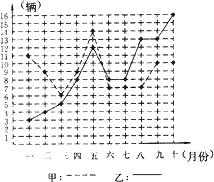
(1)请你根据上图填写下表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 5.2 | 9 | ||
乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析: ①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(k﹣1)x2﹣2x+3=0有两个不相等的实根,则k的取值范围是( )
A.k< ![]()
B.k< ![]() 且k≠1
且k≠1
C.0≤k≤ ![]()
D.k≠1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系XOY中,有A(3,2),B (﹣1,﹣4 ),P是X轴上的一点,Q是Y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句正确的是( )
A.两条直线相交,组成的图形叫做角
B.从同一点引出的两条射线组成的图形叫角
C.两条有公共点的射线组成的图形叫角
D.两条有公共端点的线段组成的图形叫角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com