
【题目】在![]() 中,
中,![]() 于点
于点![]()
(1)如图1,若![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,将
上,将![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,折痕分别为
处,折痕分别为![]() 和
和![]() ,且点
,且点![]() ,点
,点![]() 均在直线
均在直线![]() 上,若
上,若![]() ,试猜想
,试猜想![]() 与
与![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(3)在(2)小题的条件下,将![]() 绕点
绕点![]() 逆时针旋转一个角度
逆时针旋转一个角度![]() (
(![]() ),记旋转中的
),记旋转中的![]() 为
为![]() (如图3),在旋转过程中,直线
(如图3),在旋转过程中,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若
,若![]() ,是否存在这样的
,是否存在这样的![]() 两点,使
两点,使![]() 为直角三角形?若存在,请直接写出旋转角
为直角三角形?若存在,请直接写出旋转角![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.

【答案】(1)∠C=56°;(2)∠AMF=∠ANG.证明见解析;(3)满足条件的旋转角为28°或56°或208°或236°.
【解析】
(1)利用三角形的内角和定理即可解决问题;
(2)结论:∠AMF=∠ANG.由翻折可知:∠B=∠F,∠C=∠DGN,由∠B+∠C=90°,推出∠BAC=90°,∠F+∠DGN=90°,推出∠BAD+∠CAD=90°,由∠BAD=∠F+∠AMF,∠CAD=∠DGN-∠ANG,推出∠F+∠AMF+∠DGN-∠ANG=90°,可得∠AMF=∠ANG;
(3)分两种情形①当∠PQB=90°时;②当∠BPQ=90°时.分别求解即可解决问题.
解:(1)如图1中,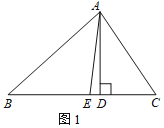
∵AD⊥BC,
∴∠ADB=∠ADC=90°
在Rt△AED中,∵∠EAD=7°,
∴∠AED=83°,
∵∠AED=∠B+∠BAE,∠B=42°,
∴∠BAE=∠CAE=41°,
∴∠BAC=82°,
∴∠C=180°-42°-82°=56°.
(2)结论:∠AMF=∠ANG.
理由:如图2中,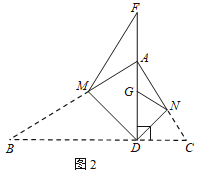
由翻折可知:∠B=∠F,∠C=∠DGN,
∵∠B+∠C=90°,
∴∠BAC=90°,∠F+∠DGN=90°,
∴∠BAD+∠CAD=90°,
∵∠BAD=∠F+∠AMF,∠CAD=∠DGN-∠ANG,
∴∠F+∠AMF+∠DGN-∠ANG=90°,
∴∠AMF=∠ANG.
(3)①如图3-1当∠PQB=90°时,
∵∠B=∠F′=28°,
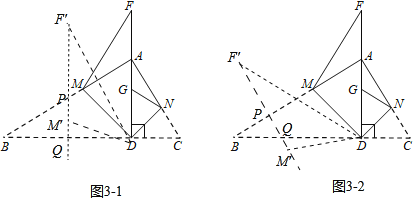
∴∠F′DQ=90°-28°=62°,
∵∠FDB=90°,
∴∠FDF′=90°-62°=28°,
∴旋转角为28°.
②如图3-2,当∠BPQ=90°时,
∵∠B=∠F′=28°,
∴∠PQB=90°-28°=62°,
∵∠PQB=∠F′+∠F′DB,
∴∠F′DB=62°-28°=34°,
∴∠FDF′=90°-34°=56°,
∴旋转角为56°,
同法可得当旋转角为208°或236°时,也满足条件,
综上所述,满足条件的旋转角为28°或56°或208°或236°.


科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
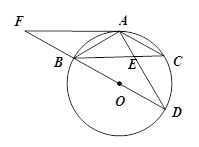
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机器零件的横截面如图所示,按要求线段AB和DC的延长线相交成直角才算合格,一工人测得∠A=23°,∠D=31°,∠AED=143°,请你帮他判断该零件是否合格:___.(填“合格”或“不合格”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 与
与![]() 成正比例,且
成正比例,且![]() 时,
时,![]() .
.
(1)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在所给的直角坐标系(如图)中画出函数的图象;
(3)直接写出当![]() 时,自变量
时,自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复![]() 下表是几次活动汇总后统计的数据:
下表是几次活动汇总后统计的数据:
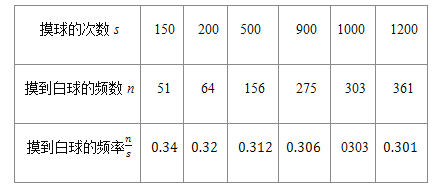
![]() 请估计:当次数s很大时,摸到白球的频率将会接近______ ;假如你去摸一次,你摸到红球的概率是______
请估计:当次数s很大时,摸到白球的频率将会接近______ ;假如你去摸一次,你摸到红球的概率是______ ![]() 精确到
精确到![]() .
.
![]() 试估算口袋中红球有多少只?
试估算口袋中红球有多少只?
![]() 解决了上面的问题后请你从统计与概率方面谈一条启示.
解决了上面的问题后请你从统计与概率方面谈一条启示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2﹣7x+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为![]() 时运动时间t的值;
时运动时间t的值;
(3)当点P运动到边AC上时,是否存在点P,使△CDP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织1000名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动.随机机取一些学生在评比中的成绩制成的统计图表如下:


根据以上图表提供的信息,解答下列问题:
(1)写出表中a、b的数值:a ,b ;
(2)补全频数分布表和频数分布直方图;
(3)如果评比成绩在95分以上(含95 分)的可以获得一等奖,试估计该校参加此次活动获得一等 奖的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】牛奶是最古老的天然饮料之一,被誉为“白色血液”,对人体的重要性可想而知,现已成为国家营养餐计划备选食品之一.为推行国家营养餐计划,某乳品公司向某营养餐中心运输不少于![]() 的牛奶.由铁路运输每千克只需运费0.58元;由公路运输,每千克需运费0.28元,还需其他费用600元.请探究并说明选用哪种运输方式所需费用较少?
的牛奶.由铁路运输每千克只需运费0.58元;由公路运输,每千克需运费0.28元,还需其他费用600元.请探究并说明选用哪种运输方式所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF是Rt△ABC的中位线,∠BAC=90°,AD是斜边BC边上的中线,EF和AD相交于点O,则下列结论不正确的是( )
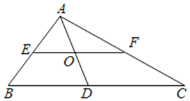
A. AO=ODB. EF=ADC. S△AEO=S△AOFD. S△ABC=2S△AEF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com