
【题目】如图,EF是Rt△ABC的中位线,∠BAC=90°,AD是斜边BC边上的中线,EF和AD相交于点O,则下列结论不正确的是( )
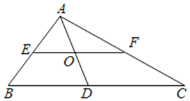
A. AO=ODB. EF=ADC. S△AEO=S△AOFD. S△ABC=2S△AEF
【答案】D
【解析】
根据三角形中位线定理以及直角三角形斜边上的中线等于斜边的一半逐项分析即可.
解:
∵EF是Rt△ABC的中位线,
∴EF![]()
![]() BC ,
BC ,
∵AD是斜边BC边上的中线,
∴AD=![]() BC,
BC,
∴EF=AD,故选项B正确;
∵AE=BE,EO∥BD,
∴AO=OD,故选项A正确;
∵E,O,F,分别是AB,AD,AC中点,
∴EO=![]() BD,OF=
BD,OF=![]() DC,
DC,
∵BD=CD,
∴OE=OF,
又∵EF∥BC,
∴S△AEO=S△AOF,故选项C正确;
∵EF∥BC,
∴△ABC∽△AEF,
∵EF是Rt△ABC的中位线,
∴S△ABC:S△AEF=4:1,
即S△ABC=4S△AEF≠2S△AEF,故选D错误,
故选:D.


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点
于点![]()
(1)如图1,若![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,将
上,将![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,折痕分别为
处,折痕分别为![]() 和
和![]() ,且点
,且点![]() ,点
,点![]() 均在直线
均在直线![]() 上,若
上,若![]() ,试猜想
,试猜想![]() 与
与![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(3)在(2)小题的条件下,将![]() 绕点
绕点![]() 逆时针旋转一个角度
逆时针旋转一个角度![]() (
(![]() ),记旋转中的
),记旋转中的![]() 为
为![]() (如图3),在旋转过程中,直线
(如图3),在旋转过程中,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若
,若![]() ,是否存在这样的
,是否存在这样的![]() 两点,使
两点,使![]() 为直角三角形?若存在,请直接写出旋转角
为直角三角形?若存在,请直接写出旋转角![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 开通了,中国联通公布了资费标准,其中包月
开通了,中国联通公布了资费标准,其中包月![]() 元时,超出部分国内拨打
元时,超出部分国内拨打![]() 元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
时间/分 | 1 | 2 | 3 | 4 | 5 | … |
电话费/元 | 0.36 | 0.72 | 1.08 | 1.44 | 1.80 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用![]() 表示超出时间,
表示超出时间,![]() 表示超出部分的电话费,那么
表示超出部分的电话费,那么![]() 与
与![]() 的关系式是什么?
的关系式是什么?
(3)如果打电话超出![]() 分钟,需多付多少电话费?
分钟,需多付多少电话费?
(4)某次打电话的费用超出部分是![]() 元,那么小明的爸爸打电话超出几分钟?
元,那么小明的爸爸打电话超出几分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A逆时针旋转80°后得到△A′B′C′(点B的对应点是点B′,点C的对应点是点C′,连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
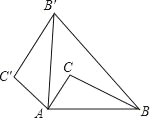
A. 82° B. 80° C. 78° D. 76°
查看答案和解析>>
科目:初中数学 来源: 题型:
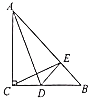
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,折叠
的平分线,折叠![]() 使得点
使得点![]() 落在
落在![]() 边上的
边上的![]() 处,连接
处,连接![]() 、
、![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 是等腰三角形;③
是等腰三角形;③![]() ;④
;④![]() .其中正确的结论是______.(填写序号)
.其中正确的结论是______.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
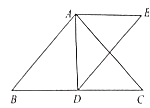
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是中线,作
是中线,作![]() 关于
关于![]() 的轴对称图形
的轴对称图形![]() .
.
(1)直接写出![]() 和
和![]() 的位置关系;
的位置关系;
(2)连接![]() ,写出
,写出![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)当![]() ,
,![]() 时,在
时,在![]() 上找一点
上找一点![]() ,使得点
,使得点![]() 到点
到点![]() 与到点
与到点![]() 的距离之和最下小,求
的距离之和最下小,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
(1)求证:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b与双曲线y=![]() 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>![]() 的解集.
的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com