
【题目】课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
科目:初中数学 来源: 题型:
【题目】某校为了进一步改进本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图. 
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( ) 
A.1:3
B.1:4
C.1:5
D.1:25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点M是BC的中点,作正方形MNPQ,使点A、C分别在MQ和MN上,连接AN、BQ.
(1)直接写出线段AN和BQ的数量关系是 .
(2)将正方形MNPQ绕点M逆时针方向旋转θ(0°<θ≤360°)
①判断(1)的结论是否成立?请利用图2证明你的结论;
②若BC=MN=6,当θ(0°<θ≤360°)为何值时,AN取得最大值,请画出此时的图形,并直接写出AQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 . 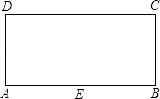
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( ) 
A.∠DAB′=∠CAB′
B.∠ACD=∠B′CD
C.AD=AE
D.AE=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB,如图,在△ABC中,AB=63m,∠A=45°,∠B=37°,求AC,CB的长.(结果保留小数点后一位)
参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() 取1.414.
取1.414.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( ) 
A.(4,3)
B.(5, ![]() )
)
C.(4, ![]() )
)
D.(5,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com