
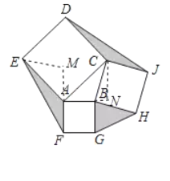
【题目】如图,以△ABC的三条边为边,分别向外作正方形,连接EF,GH,DJ,如果△ABC的面积为8,则图中阴影部分的面积为( )

A.28B.24C.20D.16
【答案】B
【解析】
过E作EM⊥FA交FA的延长线于M,过C作CN⊥AB交AB的延长线于N,根据全等三角形的性质得到EM=CN,于是得到S△AEF=S△ABC=8,同理S△CDJ=S△BHG=S△ABC=8,于是得到结论.
解:过E作EM⊥FA交FA的延长线于M,过C作CN⊥AB交AB的延长线于N,
∴∠M=∠N=90°,∠EAM+∠MAC=∠MAC+∠CAB=90°,
∴∠EAM=∠CAB
∵四边形ACDE、四边形ABGF是正方形,
∴AC=AE,AF=AB,
∴∠EAM≌△CAN,
∴EM=CN,
∵AF=AB,
∴S△AEF=![]() AFEM,S△ABC=
AFEM,S△ABC=![]() ABCN=8,
ABCN=8,
∴S△AEF=S△ABC=8,
同理S△CDJ=S△BHG=S△ABC=8,
∴图中阴影部分的面积=3×8=24,
故选:B.


科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线 y=ax2 -2ax+4(a<0) 交 x 轴于点 A、B,与 y 轴交于点 C,AB=6.
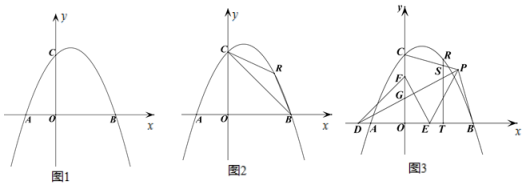
(1)如图 1,求抛物线的解析式;
(2) 如图 2,点 R 为第一象限的抛物线上一点,分别连接 RB、RC,设△RBC 的面积为 s,点 R 的横坐标为 t,求 s 与 t 的函数关系式;
(3)在(2)的条件下,如图 3,点 D 在 x 轴的负半轴上,点 F 在 y 轴的正半轴上,点 E 为 OB 上一点,点 P 为第一象限内一点,连接 PD、EF,PD 交 OC 于点 G,DG=EF,PD⊥EF,连接 PE,∠PEF=2∠PDE,连接 PB、PC,过点R 作 RT⊥OB 于点 T,交 PC 于点 S,若点 P 在 BT 的垂直平分线上,OB-TS=![]() ,求点 R 的坐标.
,求点 R 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
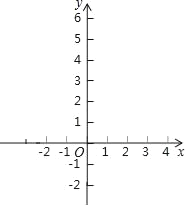
【题目】函数y=x2﹣4x+3
(1)求其图象与x轴交点A、B的坐标(A在B左边);
(2)在坐标系中画出函数图象;
(3)若函数图形的顶点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径DE⊥AB于点F,交BC于点 M,DE的延长线与AC的延长线交于点N,连接AM.
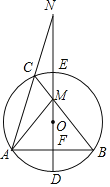
(1)求证:AM=BM;
(2)若AM⊥BM,DE=8,∠N=15°,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以点M(0, ![]() )为圆心,以
)为圆心,以![]() 长为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
长为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
(1)求出CP所在直线的解析式;
(2)连接AC,请求△ACP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
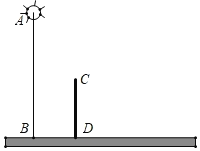
【题目】如图所示,灯在距地面6米的A处,与灯柱AB相距3米的地方有一长3米的木棒CD直立于地面.
(1)在图中画出木棒CD的影子,并求出它的长度;
(2)当木棒绕其与地面的固定端点D按顺时针方向旋转到地面时,其影子的变化有什么规律?你能求出其影长的取值范围吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com