
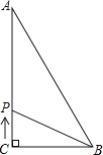
【题目】如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.

【答案】(1)6.5;(2)1:4;(3)![]() 或
或![]() .
.
【解析】
(1)根据中线的性质可知,点P在AB中点,CP把△ABC的面积分成相等的两部分,进而求解即可;
(2)求出当![]() 时,
时,![]() 与
与![]() 的长,再根据等高的三角形面积比等于底边的比求解即可;
的长,再根据等高的三角形面积比等于底边的比求解即可;
(3)分两种情况:①当P在AC上时;②当P在AB上时.
(1)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时
∵点P在AB中点
∴![]()
∴CA+AP=12+7.5=19.5(cm),
∴3t=19.5,
解得t=6.5.
故当t=6.5时,CP把△ABC的面积分成相等的两部分;
(2)5×3=15,
AP=15-12=3,
BP=15-3=12,
则S△APC:S△BPC=3:12=1:4;
(3)分两种情况:
①当P在AC上时,
∵△BCP的面积=18,
∴![]() ×9×CP=18,
×9×CP=18,
∴CP=4,
∴3t=4,
∴t=![]() ;
;
②当P在AB上时,
∵△BCP的面积=18,△ABC面积=![]() ,
,
∴![]()
∴3t=12+15×![]() =22,
=22,
解得t=![]() .
.
故t=![]() 或
或![]() 秒时,△BCP的面积为18.
秒时,△BCP的面积为18.
故答案为: ![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=8,AB=4,将此矩形折叠,使点B与点D重合,折痕为EF,连接BE、DF,以B为原点建立平面直角坐标系,使BC、BA边分别在x轴和y轴的正半轴上.

(1)试判断四边形BFDE的形状,并说明理由;
(2)求直线EF的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
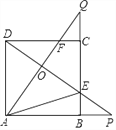
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP 交于点O,并分别与边CD,BC 交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=0E![]() OP;③
OP;③![]() ;④当BP=1时,
;④当BP=1时,![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
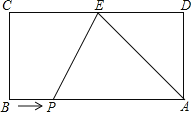
【题目】如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,P点从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为______时,∠PAE为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
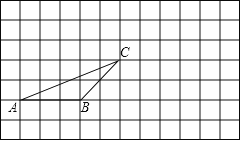
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)若格点△PAB与格点△PBC的面积相等,则这样的点P共______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=140![]() ,∠COE与∠EOD互余,OE平分∠AOD.
,∠COE与∠EOD互余,OE平分∠AOD.
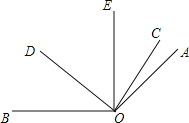
(1)若∠COE=38![]() ,求∠DOE和∠BOD的度数;
,求∠DOE和∠BOD的度数;
(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学李老师选派了班上8位同学去参加年级组的数学知识竞赛,试卷满分100分,我们将成绩中超过90分的部分记为正,低于90分的部分记为负,则这8位同学的得分如下(单位:分):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)请求出这8位同学本次数学竞赛成绩的平均分是多少?
(2)若得95分以上可以获得一等奖,请求出获得一等奖的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了从李飞与刘亮中选取一人参加市射击比赛,现将他们某次射击训练的成绩绘制了如下图所示的折线统计图:
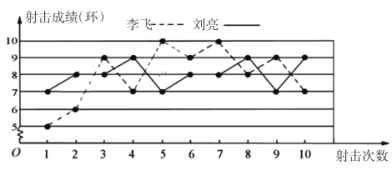
(1)请根据折线统计图中提供的信息填写下表:
平均数 | 中位 | 众数 | |
李飞 | 8 | ||
刘亮 | 8 | 8 |
(2)请计算李飞与刘亮射击训练的成绩的方差.(方差公式:![]() )
)
(3)从折线统计图上分析李飞与刘亮的射击成绩走势和稳定性,派谁去参加射击比赛更合适.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com