
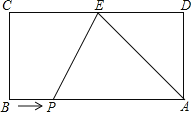
【题目】如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,P点从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为______时,∠PAE为等腰三角形?
【答案】3或2或![]() .
.
【解析】
根据矩形的性质求出∠D=90°,AB=CD=8,求出DE后根据勾股定理求出AE;过E作EM⊥AB于M,过P作PQ⊥CD于Q,求出AM=DE=3,当EP=EA时,AP=2DE=6,即可求出t;当AP=AE=5时,求出BP=3,即可求出t;当PE=PA时,则x2=(x-3)2+42,求出x,即可求出t.
∵四边形ABCD是长方形,
∴∠D=90°,AB=CD=8,
∵CE=5,
∴DE=3,
在Rt△ADE中,∠D=90°,AD=4,DE=3,由勾股定理得:AE=![]() =5;
=5;
过E作EM⊥AB于M,过P作PQ⊥CD于Q,
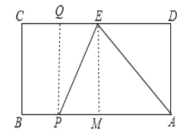
则AM=DE=3,
若△PAE是等腰三角形,则有三种可能:
当EP=EA时,AP=2DE=6,
所以t=![]() =2;
=2;
当AP=AE=5时,BP=85=3,
所以t=3÷1=3;
当PE=PA时,设PA=PE=x,BP=8x,则EQ=5(8x)=x3,
则x2=(x3)2+42,
解得:x=![]() ,
,
则t=(8![]() )÷1=
)÷1=![]() ,
,
综上所述t=3或2或![]() 时,△PAE为等腰三角形.
时,△PAE为等腰三角形.
故答案为:3或2或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
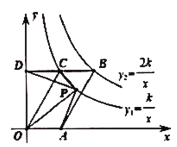
【题目】如图,□![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,
,![]() 在第一象限反比例函数
在第一象限反比例函数![]() 和
和![]() 的图象分别经过
的图象分别经过![]() 两点,延长
两点,延长![]() 交
交![]() 轴于点
轴于点![]() . 设
. 设![]() 是反比例函数
是反比例函数![]() 图象上的动点,若
图象上的动点,若![]() 的面积是
的面积是![]() 面积的2倍,
面积的2倍,![]() 的面积等于
的面积等于![]() ,则
,则![]() 的值为________。
的值为________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目 | 频数 | 频率 |
语文 |
| 0.5 |
数学 | 12 |
|
英语 | 6 |
|
物理 |
| 0.2 |

(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
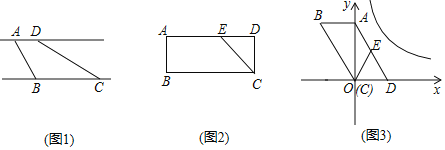
【题目】定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上,点
上,点![]() ,
,![]() 在直线
在直线![]() 上,若
上,若![]() ,则四边形
,则四边形![]() 是半对角四边形.
是半对角四边形.
(1)如图1,已知![]() ,
,![]() ,
,![]() ,若直线
,若直线![]() ,
,![]() 之间的距离为
之间的距离为![]() ,则AB的长是____,CD的长是______;
,则AB的长是____,CD的长是______;
(2)如图2,点![]() 是矩形
是矩形![]() 的边
的边![]() 上一点,
上一点,![]() ,
,![]() .若四边形
.若四边形![]() 为半对角四边形,求
为半对角四边形,求![]() 的长;
的长;
(3)如图3,以![]() 的顶点
的顶点![]() 为坐标原点,边
为坐标原点,边![]() 所在直线为
所在直线为![]() 轴,对角线
轴,对角线![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.点
轴,建立平面直角坐标系.点![]() 是边
是边![]() 上一点,满足
上一点,满足![]() .
.
①求证:四边形![]() 是半对角四边形;
是半对角四边形;
②当![]() ,
,![]() 时,将四边形
时,将四边形![]() 向右平移
向右平移![]() 个单位后,恰有两个顶点落在反比例函数
个单位后,恰有两个顶点落在反比例函数![]() 的图象上,求
的图象上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商从市场得知如下信息:
某品牌空调扇 | 某品牌电风扇 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台,设该经销商购进空调扇![]() 台,空调扇和电风扇全部销售完后获得利润为
台,空调扇和电风扇全部销售完后获得利润为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)利用函数性质,说明该经销商如何进货可获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展平后,得折痕AD,BE(如图①),点O为其交点.
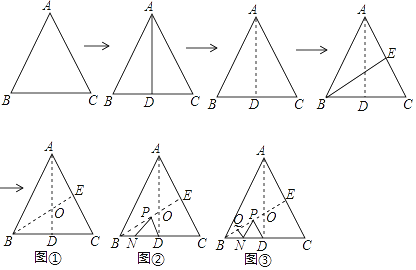
(1)探求AO到OD的数量关系,并说明理由;
(2)如图②,若P,N分别为BE,BC上的动点.
(Ⅰ)当PN+PD的长度取得最小值时,求BP的长度;
(Ⅱ)如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com