
【题目】如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展平后,得折痕AD,BE(如图①),点O为其交点.
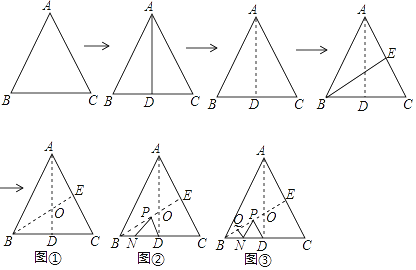
(1)探求AO到OD的数量关系,并说明理由;
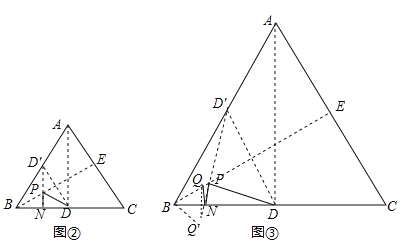
(2)如图②,若P,N分别为BE,BC上的动点.
(Ⅰ)当PN+PD的长度取得最小值时,求BP的长度;
(Ⅱ)如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值= .
【答案】(1)AO=2OD;(2)(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题(1)根据等边三角形的性质得到∠BAO=∠ABO=∠OBD=30°,得到AO=OB,根据直角三角形的性质即可得到结论;
(2)如图②,作点D关于BE的对称点D′,过D′作D′N⊥BC于N交BE于P,则此时PN+PD的长度取得最小值,根据线段垂直平分线的想知道的BD=BD′,推出△BDD′是等边三角形,得到BN=![]() BD=
BD=![]() ,于是得到结论;
,于是得到结论;
(3)如图③,作Q关于BC的对称点Q′,作D关于BE的对称点D′,连接Q′D′,即为QN+NP+PD的最小值.根据轴对称的定义得到∠Q′BN=∠QBN=30°,∠QBQ′=60°,得到△BQQ′为等边三角形,△BDD′为等边三角形,解直角三角形即可得到结论.
试题解析:解:(1)AO=2OD.理由如下:
∵△ABC是等边三角形,∴∠BAO=∠ABO=∠OBD=30°,∴AO=OB,∵BD=CD,∴AD⊥BC,∴∠BDO=90°,∴OB=2OD,∴OA=2OD;
(2)如图②,作点D关于BE的对称点D′,过D′作D′N⊥BC于N交BE于P,则此时PN+PD的长度取得最小值.∵BE垂直平分DD′,∴BD=BD′,∵∠ABC=60°,∴△BDD′是等边三角形,∴BN=![]() BD=
BD=![]() .∵∠PBN=30°,∴
.∵∠PBN=30°,∴![]() ,∴PB=
,∴PB=![]() ;
;
(3)如图③,作Q关于BC的对称点Q′,作D关于BE的对称点D′,连接Q′D′,即为QN+NP+PD的最小值.
根据轴对称的定义可知:∠Q′BN=∠QBN=30°,∠QBQ′=60°,∴△BQQ′为等边三角形,△BDD′为等边三角形,∴∠D′BQ′=90°,∴在Rt△D′BQ′中,D′Q′=![]() =
=![]() ,∴QN+NP+PD的最小值=
,∴QN+NP+PD的最小值=![]() .故答案为:
.故答案为:![]() .
.


科目:初中数学 来源: 题型:
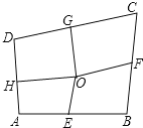
【题目】如图,四边形ABCD中,E.F.G.H依次是各边的中点,O是四边形ABCD内一点,若四边形AEOH.四边形BFOE.四边形CGOF的面积分别为10.12.14,则四边形DHOG的面积=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
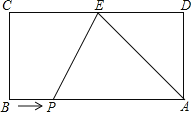
【题目】如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,P点从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为______时,∠PAE为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=140![]() ,∠COE与∠EOD互余,OE平分∠AOD.
,∠COE与∠EOD互余,OE平分∠AOD.
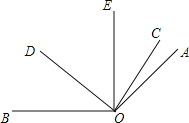
(1)若∠COE=38![]() ,求∠DOE和∠BOD的度数;
,求∠DOE和∠BOD的度数;
(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点,
内一点,![]() ,
,![]() ,点D是等边△ABC外一点,∠OCD=60°,OC=OD,连接OD、AD.
,点D是等边△ABC外一点,∠OCD=60°,OC=OD,连接OD、AD.
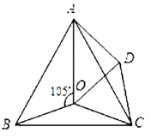
(1)求![]() 的度数(用含α的式子表示)
的度数(用含α的式子表示)
(2)求证:![]() ;
;
(3)探究:当α为多少度时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学李老师选派了班上8位同学去参加年级组的数学知识竞赛,试卷满分100分,我们将成绩中超过90分的部分记为正,低于90分的部分记为负,则这8位同学的得分如下(单位:分):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)请求出这8位同学本次数学竞赛成绩的平均分是多少?
(2)若得95分以上可以获得一等奖,请求出获得一等奖的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
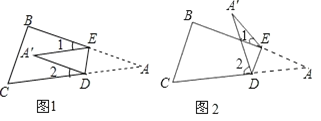
【题目】将纸片△ABC沿DE折叠使点A落在A'处的位置.
(1)如果A'落在四边形BCDE的内部(如图1),∠A'与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A'落在四边形BCDE的外部(如图2),这时∠A'与∠1、∠2之间又存在怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节日,希望通过节目的播出,能吸引更多的人关注对汉字文化的学习智慧学校开展了一次全校性的:“汉字听写”比赛,每位参赛学生听写![]() 个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数
个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数![]() 绘制成了以下不完整的统计图.
绘制成了以下不完整的统计图.
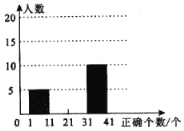
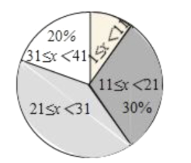
根据图表信息解答下列问题:
(1)本次共随机抽取了 名学生进行调查,听写正确的汉字个数![]() 在 范围内的人数最多,补全频数分布直方图;
在 范围内的人数最多,补全频数分布直方图;
(2)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
听写正确的汉字个数 |
|
|
|
|
组中值 |
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com