
【题目】某经销商从市场得知如下信息:
某品牌空调扇 | 某品牌电风扇 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台,设该经销商购进空调扇![]() 台,空调扇和电风扇全部销售完后获得利润为
台,空调扇和电风扇全部销售完后获得利润为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)利用函数性质,说明该经销商如何进货可获利最大?最大利润是多少元?
【答案】(1)y=140x+6000(0<x≤50);(2)购进该品牌空调扇和电风扇各50台时,经销商可获利最大,最大利润是13000元.
【解析】
(1)根据利润y=(空调扇售价﹣空调扇进价)×空调扇的数量+(电风扇售价﹣电风扇进价)×电风扇的数量,根据总资金不超过40000元得出x的取值范围,列式整理即可;
(2)利用y与x的函数关系式的增减性来选择哪种方案获利最大,并求此时的最大利润即可.
(1)y=(900﹣700)x+(160﹣100)×(100﹣x)=140x+6000,其中700x+100(100﹣x)≤40000,解得:x≤50,即y=140x+6000(0<x≤50);
(2)∵y=140x+6000,k=140>0,∴y随x的增大而增大,∴x=50时,y取得最大值,此时100﹣x=100﹣50=50(台)
又∵140×50+6000=13000,∴选择购进该品牌空调扇和电风扇各50台时,经销商可获利最大,最大利润是13000元.


科目:初中数学 来源: 题型:
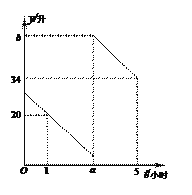
【题目】张师傅驾驶某种型号轿车从甲地去乙地,该种型号轿车每百公里油耗为10升(每行驶100公里需消耗10升汽油).途中在加油站加了一次油,加油前,根据仪表盘显示,油箱中还剩4升汽油.假设加油前轿车以80公里/小时的速度匀速行驶,加油后轿车以90公里/小时的速度匀速行驶(不计加油时间),已知油箱中剩余油量y(升)与行驶时间t(小时)之间的函数关系如图所示.
(1) 加油前,该轿车每小时消耗汔油 升;加油后,该轿车每小时消耗汔油 升;
(2)求加油前油箱剩余油量y(升)与行驶时间t(小时)之间的函数表达式;
(3)求张师傅在加油站加了多少升汽油.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线x与直线y垂直于点O,点B,C在直线x上,点A在直线x外,连接AC,AB得到△ABC.
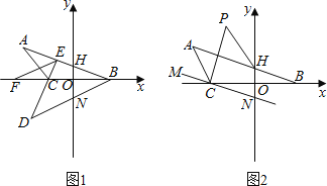
(1)将△ABC沿直线x折叠,使点A落在点D处,延长DC交AB于点E,EF平分∠AED交直线x于点F.
①若∠EFB=25°,∠DEF=10°,则∠DCF=______
②若∠ACF-∠AEF=18°,求∠EFB的度数;
(2)过点C作MN平行于AB交直线y于点N,CP平分∠BCM,HP平分∠AHY,当点C从点O沿直线x向左运动时,∠CPH的度数是否发生变化?若不变求其度数;若变化,求其变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
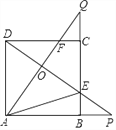
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP 交于点O,并分别与边CD,BC 交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=0E![]() OP;③
OP;③![]() ;④当BP=1时,
;④当BP=1时,![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王红有5张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最小,最小值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最大,最大值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1﹣(﹣2)]),请另写出一种符合要求的运算式子 .
查看答案和解析>>
科目:初中数学 来源: 题型:
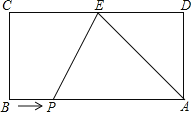
【题目】如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,P点从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为______时,∠PAE为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
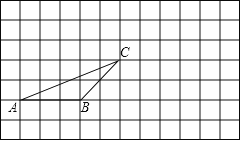
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)若格点△PAB与格点△PBC的面积相等,则这样的点P共______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=140![]() ,∠COE与∠EOD互余,OE平分∠AOD.
,∠COE与∠EOD互余,OE平分∠AOD.
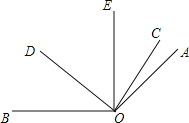
(1)若∠COE=38![]() ,求∠DOE和∠BOD的度数;
,求∠DOE和∠BOD的度数;
(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+3(1-k)(其中k为常数,k≠0),k取不同数值时,可得不同直线,请探究这些直线的共同特征.
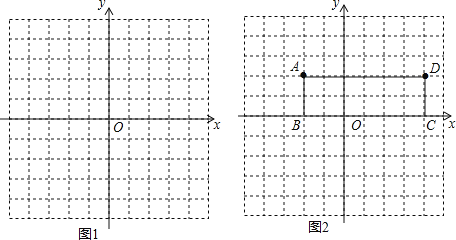
实践操作
(1)当k=1时,直线l1的解析式为 ,请在图1中画出图象;当k=2时,直线l2的解析式为 ,请在图2中画出图象;
探索发现
(2)直线y=kx+3(1-k)必经过点( , );
类比迁移
(3)矩形ABCD如图2所示,若直线y=kx+k-2(k≠0)分矩形ABCD的面积为相等的两部分,请在图中直接画出这条直线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com