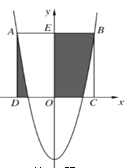
【题目】如图，二次函数y=2x2+m的图像经过点（0，-4），正方形ABCD的顶点C，D在x轴上，点A，B恰好在二次函数的图像上，则图中阴影部分的面积之和为_______.
【答案】8
【解析】
先把函数图象经过的点（0，-4）代入解析式求出m的值，再根据抛物线和正方形的对称性求出OD=OC，并判断出S阴影=S矩形BCOE，设点B的坐标为（n，2n）（n>0），把点B的坐标代入抛物线解析式求出n的值得到点B的坐标，然后求解即可．
∵二次函数y=2x2+m的图象经过点（0，-4），
∴m=-4，
∵四边形ABCD为正方形，
又∵抛物线和正方形都是轴对称图形，且y轴为它们的公共对称轴，
∴OD=OC，S阴影=S矩形BCOE，
设点B的坐标为（n，2n）（n>0），
∵点B在二次函数y=2x2-4的图象上，
∴2n=2n2-4，
解得，n1=2，n2=-1（舍负），
∴点B的坐标为（2，4），
∴S阴影=S矩形BCOE=2×4=8．
故答案为：8.
名校课堂系列答案科目：初中数学 来源： 题型：
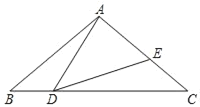
【题目】如图，等腰三角形ABC中，AB＝AC＝4，∠BAC＝100°，点D是底边BC的动点（点D不与B、C重合），连接AD，作∠ADE＝40°，DE与AC交于点E．
（1）当DC等于多少时，△ABD与△DCE全等？请说明理由；
（2）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，求出∠BDA的度数；若不可以，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
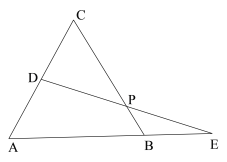
【题目】已知：如图，等边△ABC的边长为8，D为AC上的一个动点，延长AB到点E，使BE=CD，连接DE交BC于点P
（1）求证：DP=EP；
（2）若D为AC的中点，求BP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点
、
、
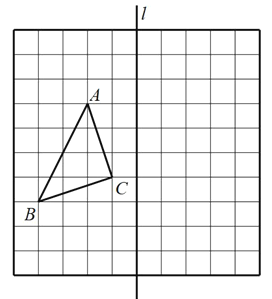
都在方格纸的格点上，方格纸中每个小正方形的边长都是1．
（1）画
关于直线
对称的
；
（2）在直线
上找一点
，使
最小；（要求在直线上标出点的位置）
（3）连接
、
，计算四边形PABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】类比转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整.
（1）尝试探究
如图（1），在正方形ABCD中，对角线AC、BD相交于点O，点E是BC边上一点，AE与BD交于点G，过点E作EF⊥AE交AC于点F，若
=2，则
的值是 ；
（2）拓展迁移
如图（2），在矩形ABCD中，过点B作BH⊥AC于点O，交AD相于点H，点E是BC边上一点，AE与BH相交于点G，过点E作EF⊥AE交AC于点F.
①若∠BAE=∠ACB，sin∠EAF=
，求tan∠ACB；
②若
，
=b（a＞0，b＞0），求的值（用含a，b的代数式表示）．
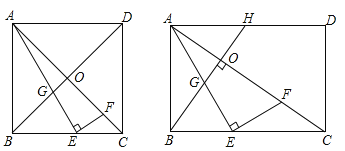
图（1） 图（2）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①所示，
是某公园的平面示意图，
分别是该公园的四个入口，两条主干道
交于点
，经测量
，
，
，请你帮助公园的管理人员解决以下问题：
（1）公园的面积为 
；
（2）如图②，公园管理人员在参观了武汉东湖绿道后，为提升游客游览的体验感，准备修建三条绿道
，其中点
在
上，点
在
上，且
（点与点
不重合），并计划在
与
两块绿地所在区域种植郁金香，求种植郁金香区域的面积；
（3）若修建（2）中的绿道每千米费用为10万元，请你画出该公园修建这三条绿道投入资金最小值时的图形．
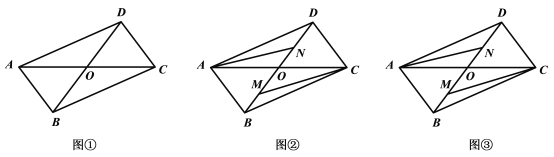
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请将下列事件发生的概率标在图中：
（1）从高处抛出的物体必落到地面；
（2）从装有
个红球的袋子中任取一个，取出的球是白球；
（3）月亮绕着地球转；
（4）从装有个红球、
个白球的口袋中任取一个球，恰好是红球（这些球除颜色外完全相同）；
（5）三名选手抽签决定比赛顺序（有三个签，分别写有
，，
），抽到写有的签．
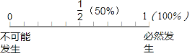
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
