
【题目】五一期间,甲、乙两人分别骑自行车和摩托车从![]() 地出发前往
地出发前往![]() 地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程
地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数图象如图所示.
之间的函数图象如图所示.

(1)甲骑自行车的速度是_____![]() .
.
(2)求乙休息后所行的路程![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
(3)为了保证及时联络,甲、乙两人在第一次相遇时约定此后两人之间的路程不超过![]() .甲、乙两人是否符合约定,并说明理由.
.甲、乙两人是否符合约定,并说明理由.
【答案】(1)0.25km/min;(2)![]() (50≤x≤110);(3)甲、乙两人符合约定.
(50≤x≤110);(3)甲、乙两人符合约定.
【解析】
(1)由图像可知,甲没有休息,匀速行驶,到终点时,行驶了30km,用了120min,即可求得其速度;
(2)首先根据图像可判定当甲走80min时,距A地20km,两人相遇,然后设乙休息后所行的路程y与x之间的函数关系为y=kx+b(k≠0),根据图像可得其经过(50,10)和(80,20)两点,列出二元一次方程组,解得即可,根据函数解析式,即可得出乙所用的时间,即得出自变量x的取值范围;
(3)根据图像信息,结合(1)和(2)的结论,判定当x=50,和x=110时,甲乙两人行驶的距离,判定两人距离差即可看是否符合约定.
解:(1)0.25km/min;
由图像可知,甲没有休息,匀速行驶,到终点时,行驶了30km,用了120min,其速度为
30÷120=0.25km/min;
(2)当甲走80min时,距A地20km,两人相遇.
设乙休息后所行的路程y与x之间的函数关系为y=kx+b(k≠0),
因为图像经过(50,10)和(80,20)两点,
由题意,得![]() ,
,
解得: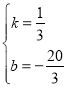 ,
,
所以y与x之间的函数关系式为![]() .
.
当y=30时,x=110.
所以自变量x的取值范围为50≤x≤110.
(3)当x=50时,甲走了12.5km,乙走了10km,12.5-10=2.5<3,符合约定.
当x=110时,甲走了27.5km,乙走了30km,30-27.5=2.5<3,符合约定.
所以甲、乙两人符合约定.


科目:初中数学 来源: 题型:
【题目】如图,把正方形纸片对折得到矩形ABCD,点E在BC上,把△ECD沿ED折叠,使点C恰好落在AD上点C′处,点M、N分别是线段AC′与线段BE上的点,把四边形ABNM沿NM向下翻折,点A落在DE的中点A′处.若原正方形的边长为12,则线段MN的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式x2﹣4>0
解:∵x2﹣4=(x+2)(x﹣2)
∴x2﹣4>0可化为
(x+2)(x﹣2)>0
由有理数的乘法法则“两数相乘,同号得正”,得
①![]() ②
②![]()
解不等式组①,得x>2,
解不等式组②,得x<﹣2,
∴(x+2)(x﹣2)>0的解集为x>2或x<﹣2,
即一元二次不等式x2﹣4>0的解集为x>2或x<﹣2.
解答下列问题:
(1)一元二次不等式x2﹣25>0的解集为 ;
(2)分式不等式![]() 的解集为 ;
的解集为 ;
(3)解一元二次不等式2x2﹣3x<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求平行四边形ACDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的对应点位置如图所示:
![]()
(1)化简:∣a∣+∣a+b∣-2∣a-b∣
(2)若a与-![]() 的距离等于b与-
的距离等于b与-![]() 的距离,求-3(a+b)+5的值.
的距离,求-3(a+b)+5的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
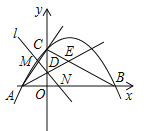
【题目】(2017南宁,第26题,10分)如图,已知抛物线![]() 与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
(1)直接写出a的值、点A的坐标及抛物线的对称轴;
(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;
(3)证明:当直线l绕点D旋转时,![]() 均为定值,并求出该定值.
均为定值,并求出该定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把一根绳子对折后得到的图形为线段AB,从点P处把绳子剪断,已知AP:BP=4:5,若剪断后的各段绳子中最长的一段为80cm,则绳子的原长为________ cm.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是AB的中点,D是BE的中点,

(1)AB=4cm,BE=3cm,则CD=____________cm;
(2)AB=4cm,DE=2cm,则AE=____________cm;
(3)AB=4cm,BE=2cm,则AD=____________cm;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com