
已知,如图,抛物线 与
与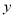 轴交于点C,与
轴交于点C,与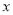 轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在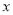 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(1) ;(2)
;(2)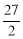 ;(3)有三个,坐标为:
;(3)有三个,坐标为: ,
,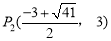 ,
,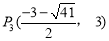 .
.
【解析】
试题分析:(1)已知了B点坐标,易求得OB、OC的长,进而可将B、C的坐标代入抛物线中,求出待定系数的值,即可得出抛物线的解析式.
(2)根据A、C的坐标,易求得直线AC的解析式.由于AB、OC都是定值,则△ABC的面积不变,若四边形ABCD面积最大,则△ADC的面积最大;可过D作x轴的垂线,交AC于M,x轴于N;易得△ADC的面积是DM与OA积的一半,可设出N点的坐标,分别代入直线AC和抛物线的解析式中,即可求出DM的长,进而可得出四边形ABCD的面积与N点横坐标间的函数关系式,根据所得函数的性质即可求出四边形ABCD的最大面积.
(3)本题应分情况讨论:①过C作x轴的平行线,与抛物线的交点符合P点的要求,此时P、C的纵坐标相同,代入抛物线的解析式中即可求出P点坐标;
②将AC平移,令C点落在x轴(即E点)、A点落在抛物线(即P点)上;可根据平行四边形的性质,得出P点纵坐标(P、C纵坐标的绝对值相等),代入抛物线的解析式中即可求得P点坐标.
试题解析:(1)∵B(1,0),∴OB=1;
∵OC=3BO,∴C(0,﹣3);
∵ 过B(1,0)、C(0,﹣3),
过B(1,0)、C(0,﹣3),
∴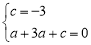 ;解这个方程组,得:
;解这个方程组,得: ,
,
∴抛物线的解析式为: .
.
(2)过点D作DM∥y轴分别交线段AC和x轴于点M、N,

在 中,令
中,令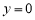 ,得方程
,得方程 ,
,
解这个方程,得 ,
,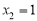 ,∴A(﹣4,0),
,∴A(﹣4,0),
设直线AC的解析式为 ,
,
∴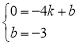 ,解这个方程组,得:
,解这个方程组,得: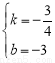 ,
,
∴AC的解析式为: ,
,
∵S四边形ABCD=S△ABC+S△ADC
=
设D( ),M(
),M( ),
),
DM= ,
,
当 时,DM有最大值3,
时,DM有最大值3,
此时四边形ABCD面积有最大值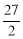 .
.
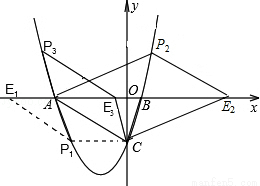
(3)如图所示,
①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形,
∵C(0,﹣3)
∴设P1(x,﹣3),∴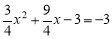 ,解得
,解得 ,
, ,∴P1(﹣3,﹣3);
,∴P1(﹣3,﹣3);
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,
∵C(0,﹣3),∴设P(x,3),∴ ,
, ,
,
解得 或
或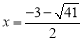 ,
,
此时存在点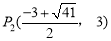 和
和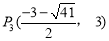 .
.
综上所述存在3个点符合题意,坐标分别是P1(﹣3,﹣3),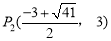 ,
,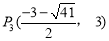 .
.
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年湖南省衡阳市八年级上学期期末考试数学试卷(解析版) 题型:填空题
若等腰三角形的顶角为80°,则它腰上的高与底边的夹角为______度.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城东台苏东双语九年级上学期第一次质量检测数学试卷(解析版) 题型:选择题
已知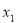 、
、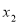 是一元二次方程
是一元二次方程 的两个根,则
的两个根,则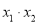 等于( )
等于( )
A.-4 B.-1 C.1 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第二次模拟数学试卷(解析版) 题型:选择题
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=( )

A.1:16 B. 1:18 C.1:20 D.1:24
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第二次模拟数学试卷(解析版) 题型:选择题
把方程x2-4x-6=0配方,化为(x+m)2=n的形式应为( )
A.(x-4)2=6 B.(x-2)2=4 C.(x-2)2=0 D.(x-2)2=10
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省九年级上学期期中考试数学试卷(解析版) 题型:解答题
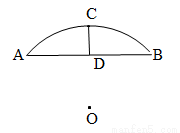
如图,某座桥的桥拱是圆弧形,它的跨度AB为8米,拱高CD为2米,求桥拱的半径.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省九年级上学期期中考试数学试卷(解析版) 题型:填空题
圣诞节时,一个小组有x人,他们每两人之间互送贺卡一张,已知全组共送贺卡132张,则可列方程为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏东台苏东双语八年级上学期第一次质检数学试卷(解析版) 题型:解答题
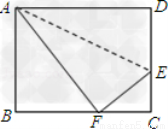
如图,折叠长方形(四个角都是直角,对边相等)的一边AD使点D落在BC边的点F处,已知AB = 8cm,BC = 10 cm,求EC的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com