
如图,折叠长方形(四个角都是直角,对边相等)的一边AD使点D落在BC边的点F处,已知AB = 8cm,BC = 10 cm,求EC的长
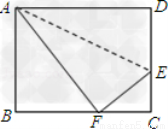
CE=3cm
【解析】
试题分析:要求CE的长,应先设CE的长为x,由将△ADE折叠使点D恰好落在BC边上的点F可得Rt△ADE≌Rt△AEF,所以AF=10cm,EF=DE=8-x;在Rt△ABF中由勾股定理得:AB2+BF2=AF2,已知AB、AF的长可求出BF的长,又CF=BC-BF=10-BF,在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,即:(8-x)2=x2+(10-BF)2,将求出的BF的值代入该方程求出x的值,即求出了CE的长.
试题解析:根据题意得:Rt△ADE≌Rt△AEF,
∴∠AFE=90°,AF=10cm,EF=DE,
设CE=xcm,则DE=EF=CD-CE=8-x,
在Rt△ABF中由勾股定理得:AB2+BF2=AF2,
即82+BF2=102,
∴BF=6cm,
∴CF=BC-BF=10-6=4(cm),
在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,
即(8-x)2=x2+42,
∴64-16x+x2=x2+16,
∴x=3(cm),
即CE=3cm.
考点:1.勾股定理;2.翻折变换(折叠问题).


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源:2014-2015学年广东省九年级上学期期中考试数学试卷(解析版) 题型:解答题
已知,如图,抛物线 与
与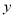 轴交于点C,与
轴交于点C,与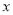 轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在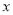 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省宣城市泾县琴溪片九年级上学期期中联考数学试卷(解析版) 题型:选择题
如图所示,抛物线y=ax2-x+c 的对称轴是直线x=1
的对称轴是直线x=1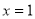 ,且图像经过点
,且图像经过点 (3,0),则
(3,0),则 的值为( )
的值为( )
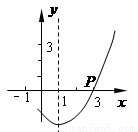
A、0 B、 -1 C、 1 D、 2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津宝坻王卜庄镇初中八年级上学期期中考试数学试卷(解析版) 题型:选择题
在△ABC中,∠A=39°,∠B=41°,则∠C的度数为( )
A.70° B.80° C.90° D.100°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏东台苏东双语八年级上学期第一次质检数学试卷(解析版) 题型:解答题
如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:(1)①②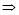 ③;(2)①③
③;(2)①③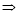 ②;(3)②③
②;(3)②③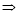 ①.
①.

(1)以上三个命题是真命题的为(直接写号) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏启东南苑中学七年级上学期第一单元测试数学试卷(解析版) 题型:解答题
宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com