
【题目】已知:△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点M是BE的中点,连接CM、DM.

(1)当点D在AB上,点E在AC上时(如图一),求证:DM=CM,DM⊥CM;
(2)当点D在CA延长线上时(如图二)(1)中结论仍然成立,请补全图形(不用证明);
(3)当ED∥AB时(如图三),上述结论仍然成立,请加以证明.
【答案】(1)证明见解析;(2)见解析;(3)见解析.
【解析】
(1)如图一中,延长![]() 使得
使得![]() ,连接
,连接![]() 、
、![]() ,先证明
,先证明![]() ,再证明
,再证明![]() 即可解决问题.
即可解决问题.
(2)补充图形如图二所示,延长![]() 交
交![]() 的延长线于
的延长线于![]() ,只要证明
,只要证明![]() ,再证明
,再证明![]() 是等腰直角三角形即可.
是等腰直角三角形即可.
(3)如图三中,如图一中,延长![]() 使得
使得![]() ,连接
,连接![]() 、
、![]() ,
,![]() ,先证明
,先证明![]() ,再证明
,再证明![]() 即可.
即可.
(1)证明:如图一中,延长DM使得MN=DM,连接BN、CN.

在△DME和△NMB中, ,
,
∴△DME≌△NMB,
∴DE=BN,∠MDE=∠MNB,
∴DE∥NB,
∴∠ADE=∠ABN=90°,
∵△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,
∴AD=DE=BN,AC=BC,∠A=∠ABC=45°,
∴∠CBN=45°=∠A,
在△ACD和△BCN中,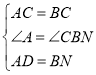 ,
,
∴△ACD≌△BCN,
∴DC=CN,∠ACD=∠BCN,
∴∠DCN=∠ACB=90°,
∴△DCN是等腰直角三角形,
DM=MN,
∴DM=CM.DM⊥CM
(2)解:如图二所示
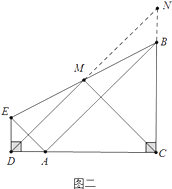
延长DM交CB的延长线于N, ∵△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,
∴AD=DE=BN,AC=BC,∠A=∠ABC=45°,
∵∠EDC+∠DCN=180°,
∴DE∥CN,
∴∠EDM=∠N
在△DME和△NMB中, ,
,
∴△DME≌△NMB,
∴DE=BN=AD,DM=MN,
∴CD=CN,
∴∠CDN=∠N=45°,CM=DM=MN,CM⊥DN,
∴DM=CM.DM⊥CM.
(3)证明:如图三中,如图一中,延长DM交AB于N连接CN.

∵DE∥AB,
∴∠MBN=∠MED,
在△DME和△NMB中,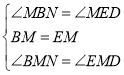 ,
,
∴△DME≌△NMB,
∴DE=BN=AD,DM=MN,
∵△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,
∴AD=DE=BN,AC=BC,∠BAC=∠ABC=45°,
∵∠AED+∠BAE=180°,
∴∠BAE=135°,
∵∠BAC=∠EAD=45°,
∴∠DAC=∠CBN=45°
在△ACD和△BCN中, ,
,
∴△ACD≌△BCN,
∴DC=CN,∠ACD=∠BCN,
∴∠DCN=∠ACB=90°,
∴△DCN是等腰直角三角形,∵DM=MN,
∴DM=CM.DM⊥CM


科目:初中数学 来源: 题型:
【题目】一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;
①若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
②若AB为任意值,且①中的S的值为定值,求a与b的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点O是对角线AC上一点,连接BO、DO,△COD、△AOD、△AOB、△BOC的面积分别是S1、S2、S3、S4.下列关于S1、S2、S3、S4的等量关系式中错误的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,在△ABC内求作一点O,使点O到三边的距离相等.甲同学的作法如图1所示,乙同学的作法如图2所示,对于两人的作法,下列说法正确的是( )
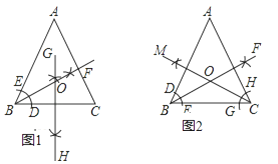
A.两人都对B.两人都不对C.甲对,乙不对D.乙对,甲不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆. 
(1)求证:AB是⊙O的切线;
(2)若AC=8,tan∠BAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=40°,∠C=110°.按要求完成下列各题.
(1)画出△ABC的高AD;
(2)画出△ABC的角平分线AE;
(3)根据你所画的图形求∠DAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图形的操作过程:
在图①中,将线段A1A2向右平移1个单位到B1B2 , 得到封闭图形A1A2B2B1(即阴影部分);
在图②中,将折线A1A2A3向右平移1个单位到B1B2B3 , 得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影; 
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:
S1= , S2= , S3= .
(3)联想与探索:
如图④在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少并说明你的猜想是正确的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com